Математика
Как найти область определения функции?
 |
Синонимы: область допустимых значений или сокращенно ОДЗ. Первое, с чем Вы сталкиваетесь при изучении различных функций или же при построении графиков - это область определения функции. Определение:Областью определения называется множество значений, которые может принимать x. Обозначение D(f).Как же это правило применить к заданной Вам функции? |
Исследование функции и построение графика функции
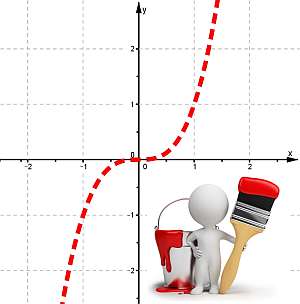 |
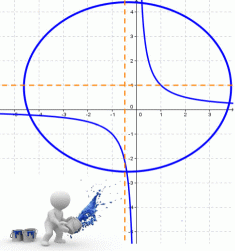
Для того, чтобы построить график функции необходимо провести полное исследование заданной функции. Затем поэтапно, используя полученные результаты, построить график.Как построить график функции?После краткого описания пунктов исследования, приведем ряд примеров по теме построения графиков функции с полным предварительным исследованием.
|
Кривые второго порядка
|
|
Кривая второго порядка - это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением: |
Как решить транспортную задачу?
 |
В данной статье разберемся с решением транспортной задачи. Все действия будем выполнять пошагово с очень подробными пояснениями. Дадим определение, аналогичное тому, которое дано в ваших учебниках или лекциях. Определение:Транспортная задача - это математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов с минимизацией затрат на перемещение. |
Где построить график функции?
 |
Раньше, когда все работы выполнялись в тетрадках, такого вопроса, где построить график функции (в каком редакторе) не возникало. Сейчас нам больше нравится тыкать на кнопки клавиатуры, нежели писать ручками. Оформленная на компьютере работа выглядит аккуратно, а если немного приноровиться, то скорость выполнения будет выше рукописной.
Каждый из нас знает в каком редакторе набрать текст, но вот с графиками дело обстоит чуть хуже. Я использую для этих целей Geogebra. Определение с Википедии: GeoGebra — свободно распространяемая (GPL) динамическая геометрическая среда, которая даёт возможность создавать чертежи в планиметрии, в частности, для построений с помощью циркуля и линейки. Скачать ее можно тут совершенно бесплатно: http://www.geogebra.org/cms/ru/ |
Открытая транспортная задача. Как решить?
 |
Будем считать, что мы уже знаем, что такое транспортная задача, как решить закрытую транспортную задачу, как составить первоначальный опорный план и как бороться с вырожденностью плана. Если что - то из этого Вам незнакомо, то при желании можно изучить тут:Как решить транспортную задачу? Вырожденность опорного плана транспортной задачи. Как избавиться? Транспортная задача называется открытой, если не соблюдается баланс между объемом спроса и объемом предложения. Например, если запасы на всех складах меньше или больше потребностей всех магазинов - потребителей, то имеем дело с открытой транспортной моделью. |
Для того, чтобы применить к задаче метод потенциалов, необходимо привести открытую транспортную задачу к закрытой модели. Т.е. необходимо выполнить преобразования, при которых , "то, что есть, станет равным, тому, что надо".
Вырожденность опорного плана транспортной задачи. Как избавиться?
 |
Чтобы не попасть в тупик при решении транспортной задачи, необходимо иметь представление о вырожденности и невырожденности опорного плана. Опорный план транспортной задачи называется невырожденным, если число базисных ячеек равно r=n+m-1, где m - количество строк, n - количество столбцов транспортной задачи. Если число перевозок меньше чем r=n+m-1, то такой план называется вырожденным. |
На начальном этапе решения транспортной задачи необходимо получить первоначальный опорный план. Как это сделать, подробно описано в статье Как решить транспортную задачу. После получения опорного плана необходимо проверить его на невырожденность.
Графики функций. Простейшие построения. Прямая на плоскости
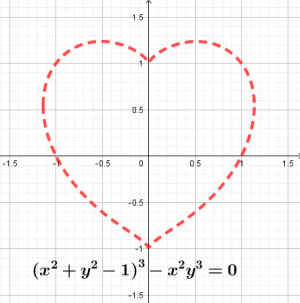 |
График функции - это наглядный образ некоторой функции f(x). Здесь каждому значению х соответствует единственное значение y. Это множество точек на плоскости, координаты которых удовлетворяют заданному уравнению y = f(x).График уравнения - это множество всех точек плоскости, которые удовлетворяют заданному уравнению, т.е. обращают уравнение в верное числовое равенство. Зависимость в данном случае не обязательно является функцией.Рассмотрим ряд элементарных функций, таких, как прямая, парабола, гипербола, их свойства и правила построения. |