Открытая транспортная задача. Как решить?
 |
Будем считать, что мы уже знаем, что такое транспортная задача, как решить закрытую транспортную задачу, как составить первоначальный опорный план и как бороться с вырожденностью плана. Если что - то из этого Вам незнакомо, то при желании можно изучить тут:Как решить транспортную задачу? Вырожденность опорного плана транспортной задачи. Как избавиться? Транспортная задача называется открытой, если не соблюдается баланс между объемом спроса и объемом предложения. Например, если запасы на всех складах меньше или больше потребностей всех магазинов - потребителей, то имеем дело с открытой транспортной моделью. |
Для того, чтобы применить к задаче метод потенциалов, необходимо привести открытую транспортную задачу к закрытой модели. Т.е. необходимо выполнить преобразования, при которых , "то, что есть, станет равным, тому, что надо".
Все очень просто. Если не хватает товара, чтобы удовлетворить потребности магазинов, нужно добавить мнимого (фиктивного) поставщика. Если предложение превышает над спросом, добавим мнимого (фиктивного) потребителя.
В открытой транспортной задаче это реализуется добавлением строки или столбца, в зависимости от того,чего не хватает. Так как в реальности фиктивный поставщик (потребитель) не существует, то стоимость доставки до него от любого пункта равна нулю.
Чтобы привести открытую транспортную задачу к закрытому (замкнутому) виду, добавляем столбец (строку) с нулевыми стоимостями.
-
Если превышают запасы - добавляем фиктивного потребителя (столбец)
-
Если превышает спрос - добавляем фиктивного поставщика (строку)
Рассмотрим подробно на примере.
Открытая транспортная задача - пример 1:
Решить транспортную задачу с исходными данными:

Общие потребности (спрос) = 40 + 180 + 80 + 60 = 360
Общие запасы (предложение) = 120 + 100 = 220
Видим, что спрос превышает над предложением.
Следовательно добавляем фиктивного поставщика А3 с объем запасов 360 - 220 = 140.

Получили закрытую транспортную задачу: спрос = предложению.
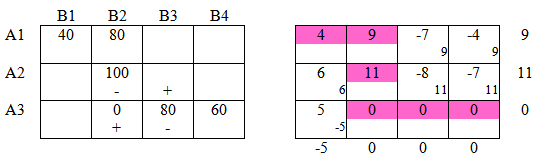
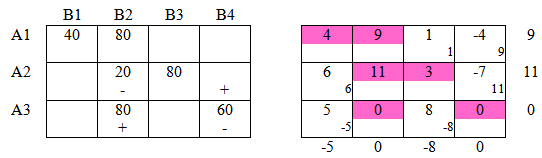
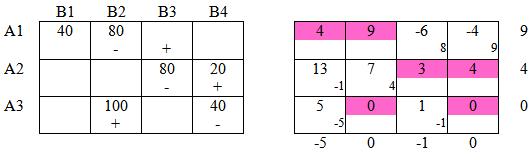
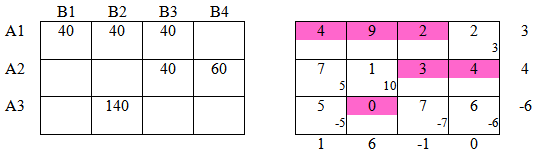
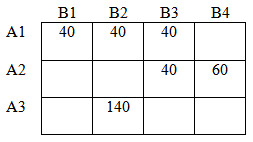
Построим первоначальный план методом северо-западного угла: Шаг 1: Проверим первоначальный план на оптимальность: Подробно о том, как были заполнены таблицы можно посмотреть тут: Как решить транспортную задачу? Среди оценочных значений правой таблице есть отрицательные, следовательно план не оптимален. Построили замкнутую цепочку знаков " + " и " — ". Среди ячеек, помеченных " — " выберем ячейку с минимальным значением: К = min{80;100}=80 Это значение 80 перенесем в пустую ячейку, помеченную " + ", далее, к значениям в ячейках с " + " прибавим К, из значений в ячейках с " — " вычтем К. Определим стоимость перевозки на первом шаге: S1 = 40 · 4 + 80 · 9 + 100 · 11 + 0 · 0 + 80 · 0 + 60 · 0 = 1980 Шаг 2: К = min{20;60}=20 Среди оценочных значений правой таблице есть отрицательные, следовательно план не оптимален. В ячейках с " + " прибавим данное значение, в ячейках с " — " вычтем. Общая стоимость перевозки на данном шаге: S2 = 40 · 4 + 80 · 9 + 20 · 11 + 80 · 3 + 80 · 0 + 60 · 0 = 1340 < S1 Видим, что стоимость перевозки на текущем шаге меньше чем на предыдущем. Шаг 3: К = min{80;40}=40 Среди оценочных значений правой таблице есть отрицательные, следовательно план не оптимален. Общая стоимость перевозки на данном шаге: S3 = 40 · 4 + 80 · 9 + 80 · 3 + 20 · 4 + 100 · 0 + 40 · 0 = 1200 < S2 Видим, что стоимость перевозки на текущем шаге меньше чем на предыдущем. Шаг 4: Среди оценочных значений нет отрицательных, следовательно решение оптимально. S4 = 40 · 4 + 40 · 9 + 40 · 2 + 40 · 3 + 60 · 4 + 140 · 0 = 960 < S3 Задача решена, получен оптимальный план перевозок. 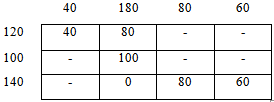
Открытая транспортная задача - пример 2:
Решить открытую транспортную задачу с исходными данными:
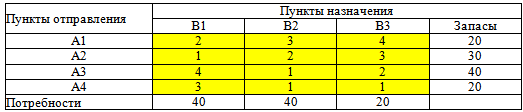
Общие потребности (спрос) = 40 + 40 + 20 = 100
Общие запасы (предложение) = 20 + 30 + 40 + 20 = 110
Видим, что предложение превышает над спросом.
Следовательно добавляем фиктивного потребителя В4 с потребностями 110 - 100 = 10.
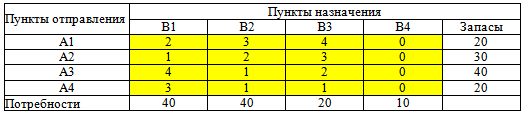
Получили закрытую транспортную задачу: спрос = предложению.