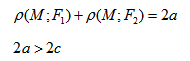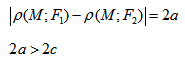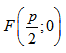Кривые второго порядка
|
|
Кривая второго порядка - это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением: |
Покажем на примере определение значений коэффициентов.
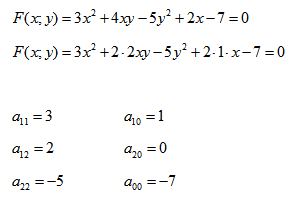
Рассмотрим кривую второго порядка:
Вычислим определитель из коэффициентов:
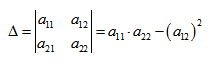
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
если Δ < 0, кривая второго порядка гиперболического типа.
Эллипс - множество точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 есть величина постоянная, большая расстояния между этими точками.
F1 и F2 - фокусы.
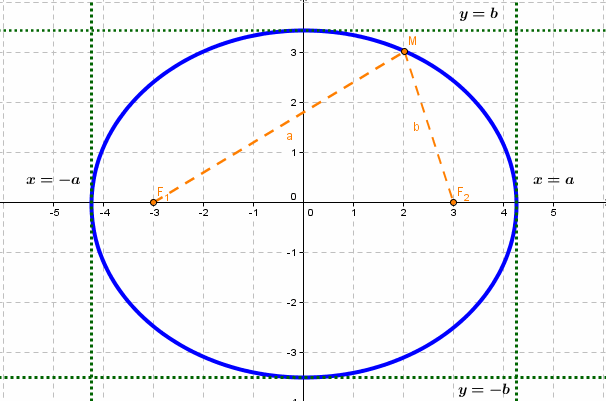 |
с - фокальное расстояние, F1(-c;0) - левый фокус, F2(c;0) - правый фокус.
|
Каноническое уравнение эллипса с центром симметрии в начале координат:
![]()
2а - большая ось эллипса, 2b - малая ось эллипса.
а - большая полуось эллипса, b - малая полуось эллипса.
Если a = b, то имеем окружность с радиусов R = a = b:
![]()
Если центр эллипса находится не в начале координат, а в некоторой точке C(x0;y0), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:
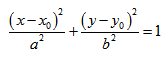
Эксцентриситет - число, равное отношению фокального расстояния к большей полуоси:
![]()
Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.
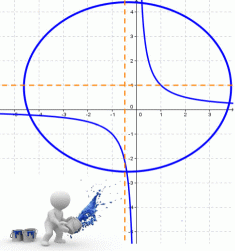
Гипербола - множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
F1 и F2 - фокусы.
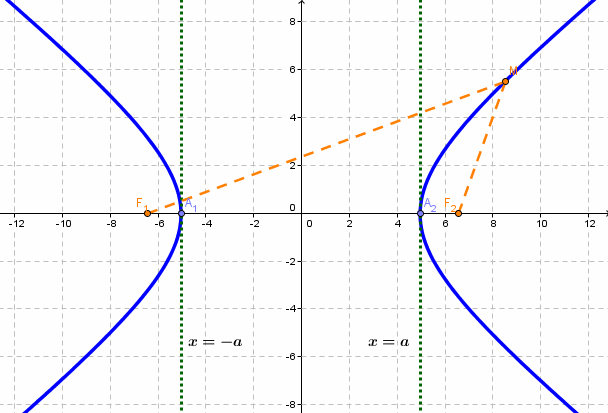 |
с - фокальное расстояние, F1(-c;0) - левый фокус, F2(c;0) - правый фокус. А1(-а;0), А2(а;0) - вершины.
|
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
Каноническое уравнение гиперболы с центром симметрии в начале координат:

x - действительная ось, y - мнимая ось.
а - действительная полуось, b - мнимая полуось.
Если центр гиперболы находится в некоторой точке C(x0;y0), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:
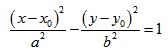
Эксцентриситет гиперболы - число, равное отношению фокусного расстояния к действительной полуоси.
![]()
Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.
Директриса гиперболы - прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.
f1 - правая директриса, f2 - левая директриса.
Уравнения директрис:
![]()
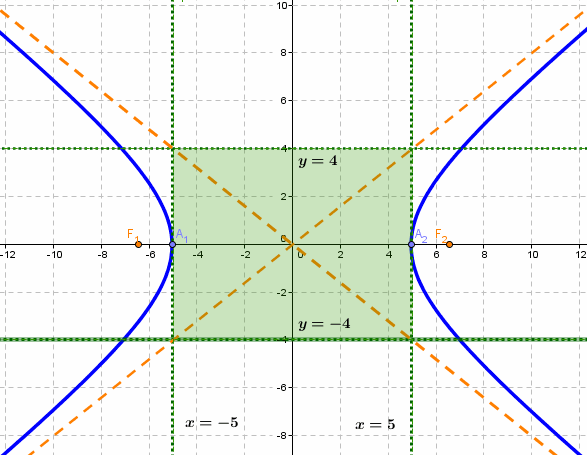
Порядок построения гиперболы:
1. Строим прямоугольник со сторонами 2a и 2b.
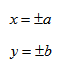
2. Провести асимптоты гиперболы - диагонали построенного прямоугольника.
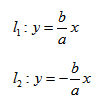
3. Строим гиперболу с вершинами в точках А1(-а;0), А2(а;0).
 |
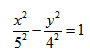 |
Парабола - множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F - фокус параболы, f - директриса параболы.
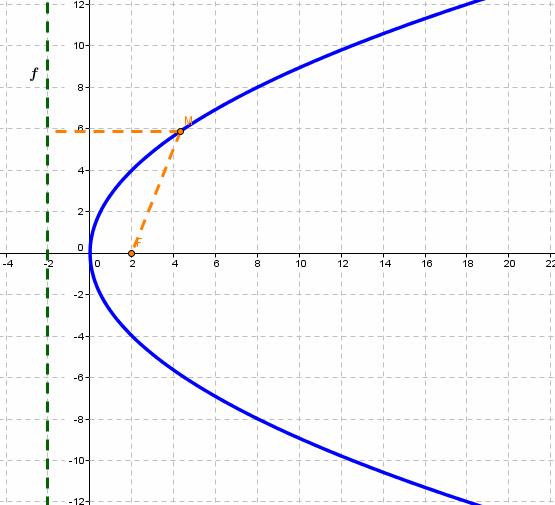 |
р - фокальное расстояние Фокус параболы:
Директриса параболы:
|
Пример по теме кривые второго порядка №1
Привести к каноническому виду и построить график кривой второго порядка.
![]()
Пример по теме кривые второго порядка №2
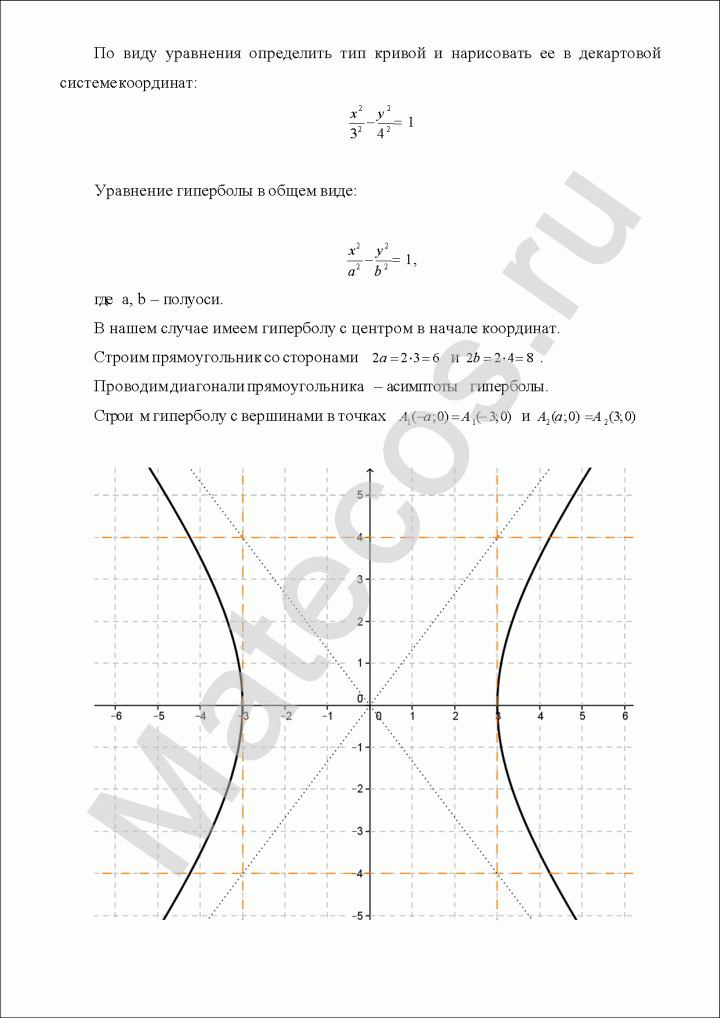
По виду уравнения определить тип кривой и нарисовать ее в декартовой системе координат:
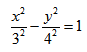
Пример по теме кривые второго порядка №3
Построить кривую второго порядка:
![]()
Пример по теме кривые второго порядка №4
Построить кривую второго порядка:
![]()
Пример по теме кривые второго порядка №5
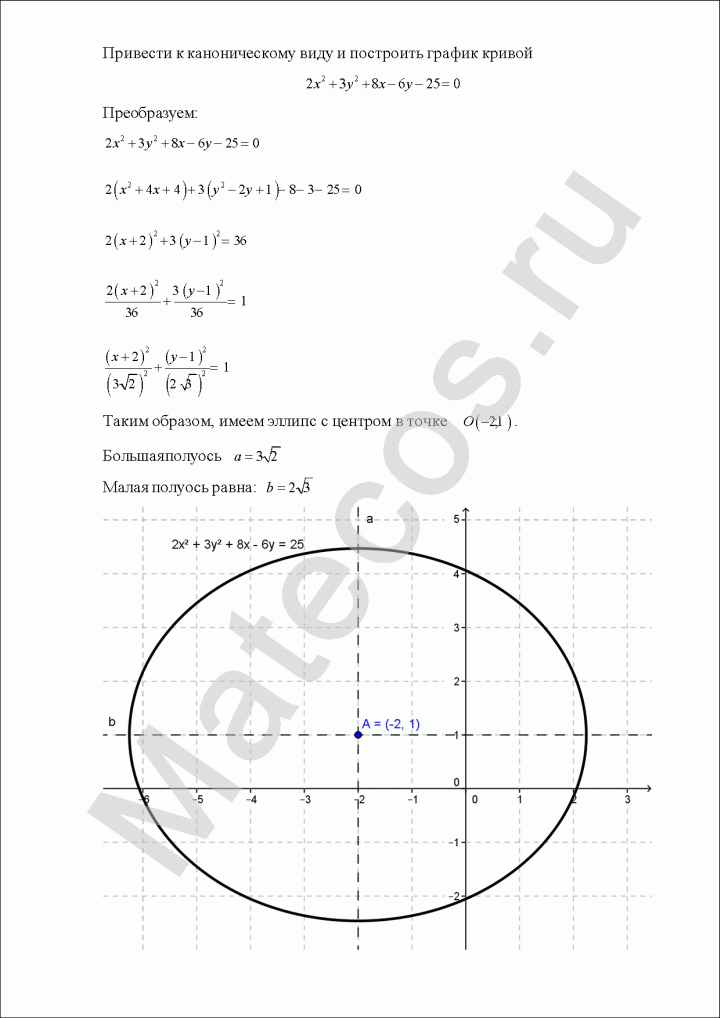
Провести заданное уравнение линии второго порядка к каноническому виду и построить ее:
![]()
Пример по теме кривые второго порядка №6
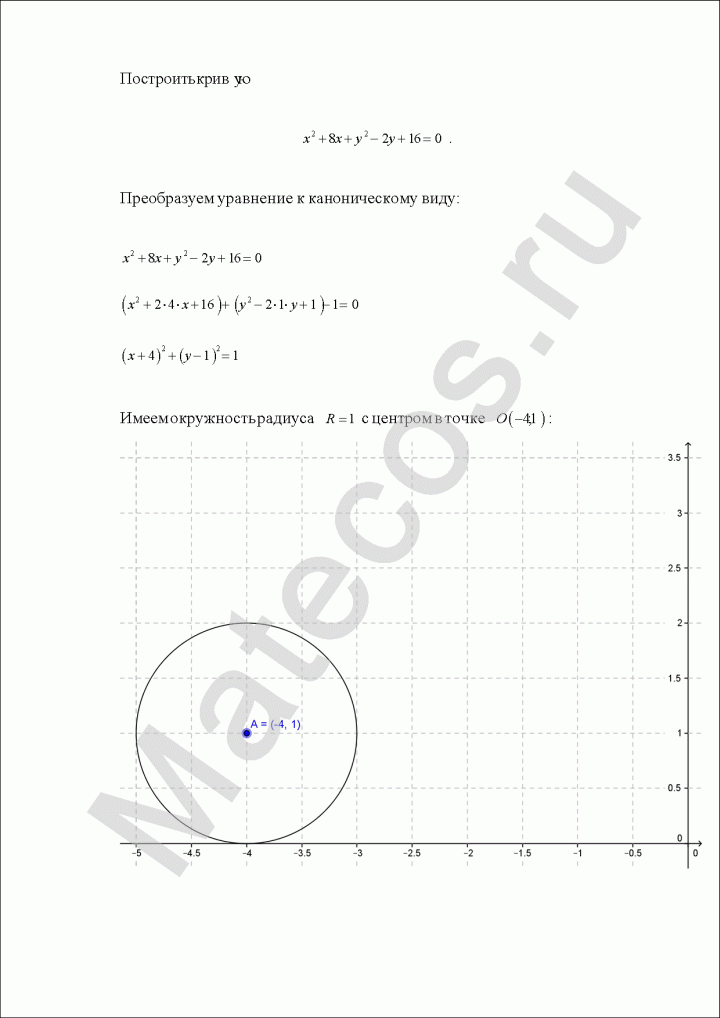
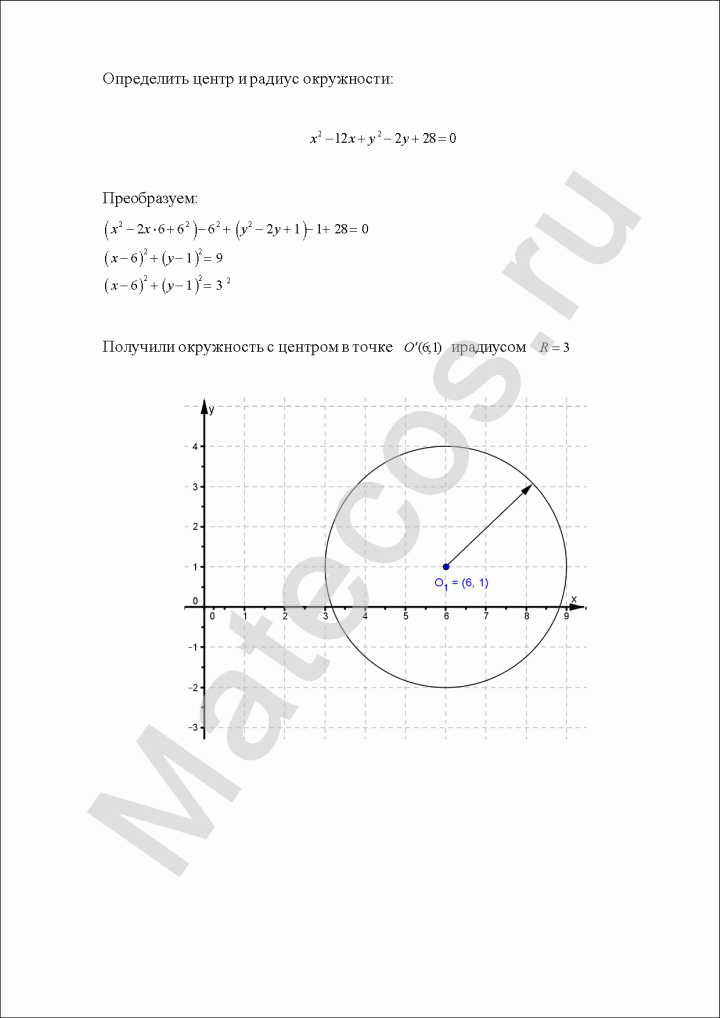
Определить центр и радиус окружности:
![]()
Пример по теме кривые второго порядка №7
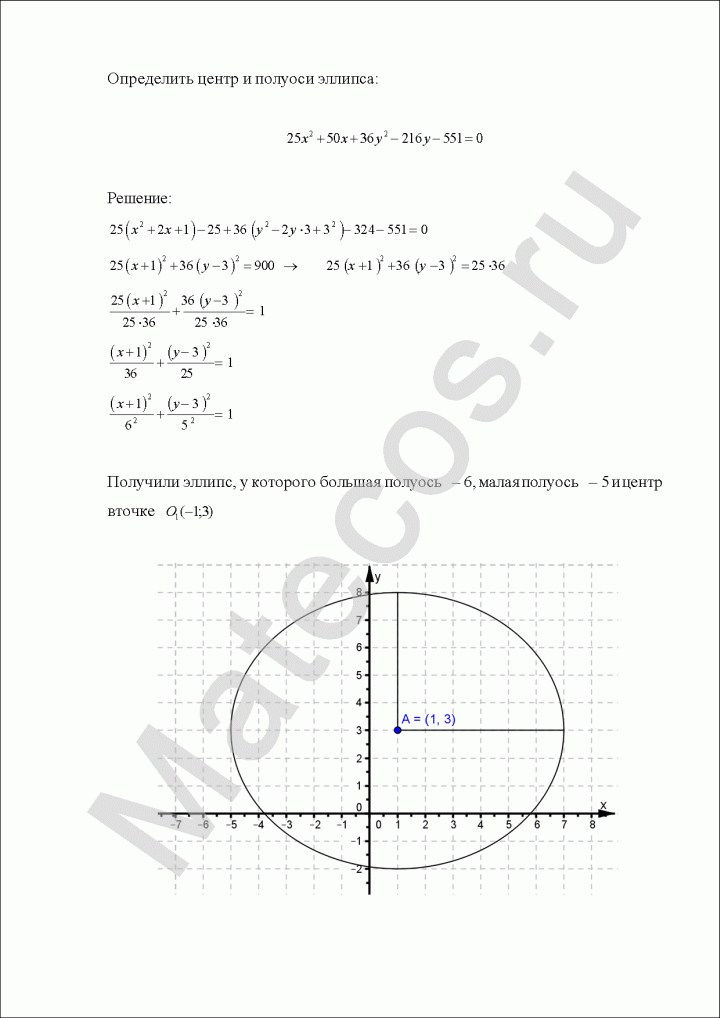
Определить центр и полуоси эллипса:
![]()
Пример по теме кривые второго порядка №8
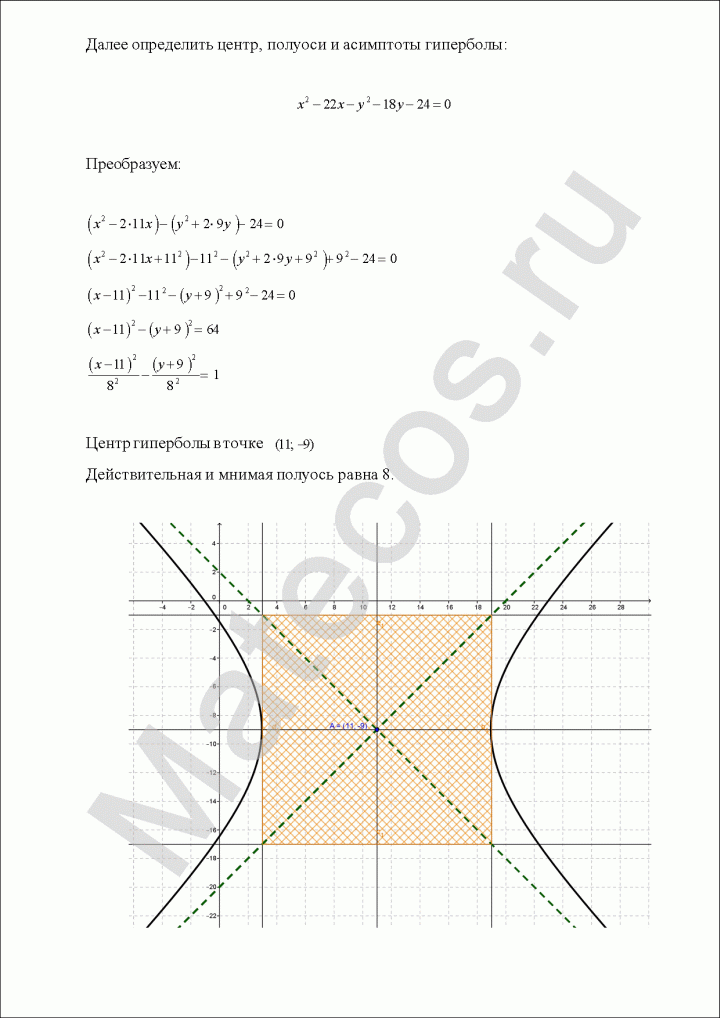
Определить центр, полуоси и асимптоты гиперболы:
![]()
Пример по теме кривые второго порядка №9
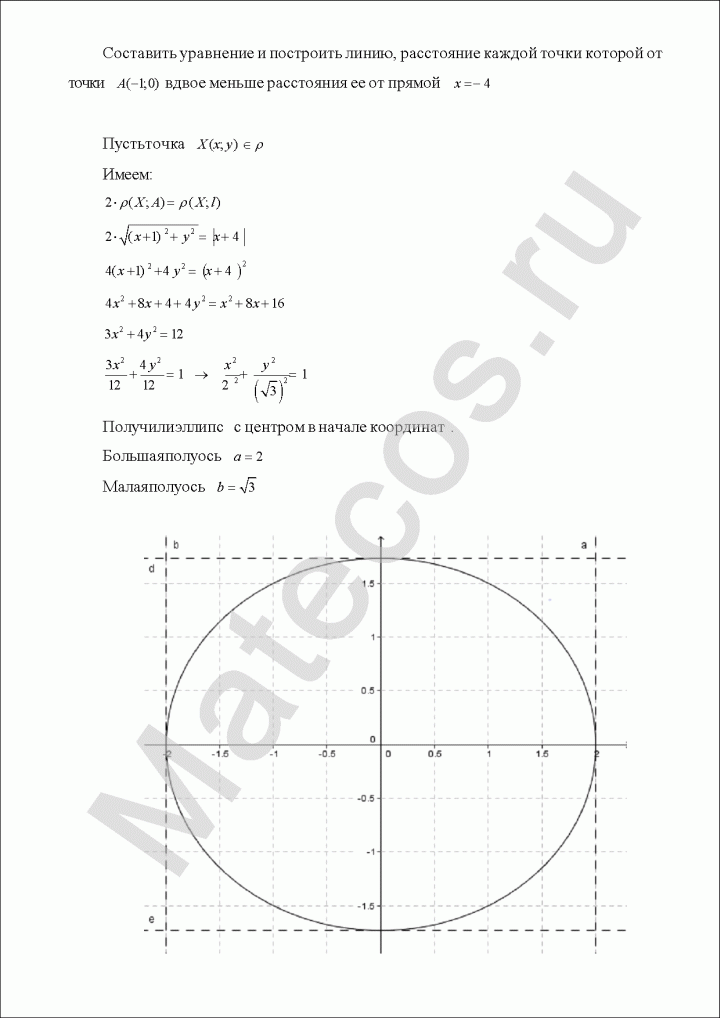
Составить уравнение и построить линию, расстояние каждой точки которой от точки A(-1;0) вдвое меньше расстояния ее от прямой x=-4
Пример по теме кривые второго порядка №10
Определить тип кривой второго порядка:
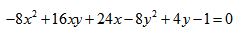
Пример по теме кривые второго порядка №11
Дана кривая:
![]()
Докажите, что эта кривая – эллипс.
Найдите координаты центра симметрии.
Найдите его большую и малую полуоси.
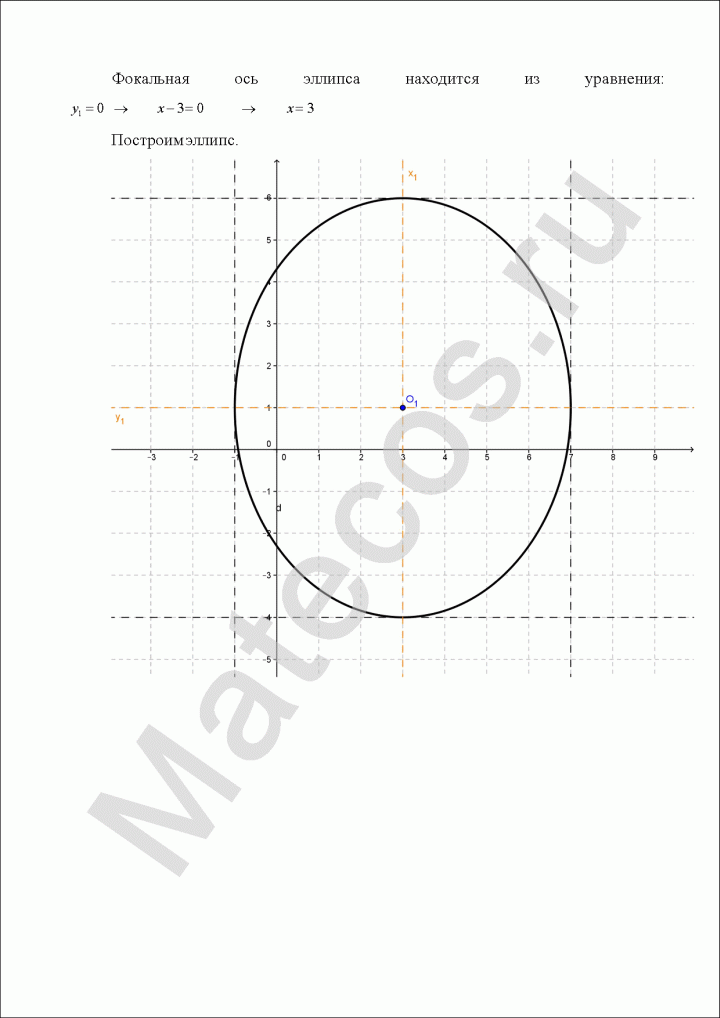
Запишите уравнение фокальной оси.
Постройте данную кривую.
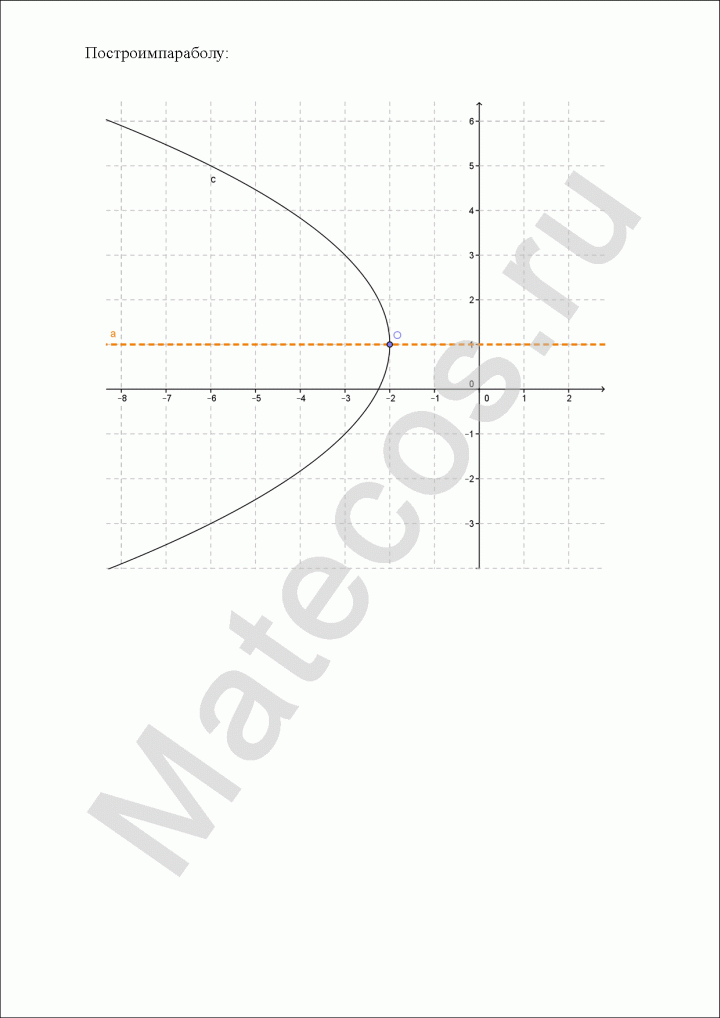
Пример по теме кривые второго порядка №12
Дана кривая:
![]()
Доказать, что данная кривая – парабола.
Найти координаты вершины параболы.
Найдите значение ее параметра.
Запишите уравнение оси симметрии параболы.
Постройте данную параболу.
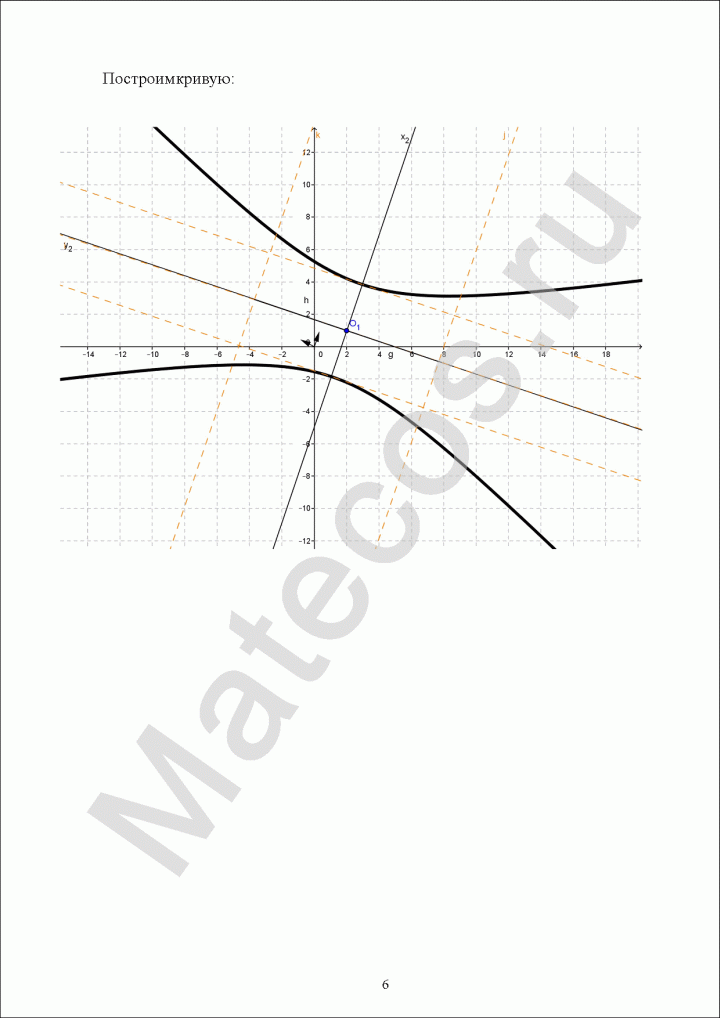
Пример по теме кривые второго порядка №13
Дана кривая:
![]()
Докажите, что кривая – гипербола.
Найдите координаты центра симметрии гиперболы.
Найдите действительную и мнимую полуоси гиперболы.
Запишите уравнение фокальной оси гиперболы.
Найдите данную гиперболу.
Пример по теме кривые второго порядка №14