Задача по статистике S-7

Изменение численности работающих характеризуется следующими данными:

1.Определить вид динамического ряда.
2.Определить аналитические показатели динамики: абсолютный прирост, темп роста и прироста (цепные и базисные), абсолютное содержание 1% прироста. Результаты оформить таблицей.
3.Определить динамические средние за период.
4.Для определения тенденции изменения численности работающих произведите аналитическое выравнивание и выразите общую тенденцию соответствующим математическим уравнением.
5.Определить выровненные (теоретические) уровни ряда динамики и нанести их на график – с фактическими данными.
6.Предполагая, что выявленная тенденция сохранится в будущем, определить ожидаемую численность работающих на ближайшие 5 лет.

Решение:
Для наглядности построим гистограмму.

Имеем дело с моментным рядом динамики с равноотстоящими уровнями.
Абсолютные приросты определяются как разность между двумя уровнями динамического ряд и показывают, насколько данный уровень превышает уровень, принятый за базу сравнения.
Базисные абсолютные приросты определяются при сравнении с переменной базой (базисный период), по формуле:

Цепные абсолютные приросты определяются при сравнении с переменной базой, по формуле:

Рассчитываем базисные абсолютные приросты, за базисный период принимаем 1 год (1983) и соответствующее ему значение численности 746

Определим среднегодовой темп роста.
Относительные величины динамики принято называть темпами роста – темпами динамики (Т).
Цепные темпы роста

Базисные темпы роста - за основу принимается постоянная база сравнения, т.е. начальный уровень ряда динамики.

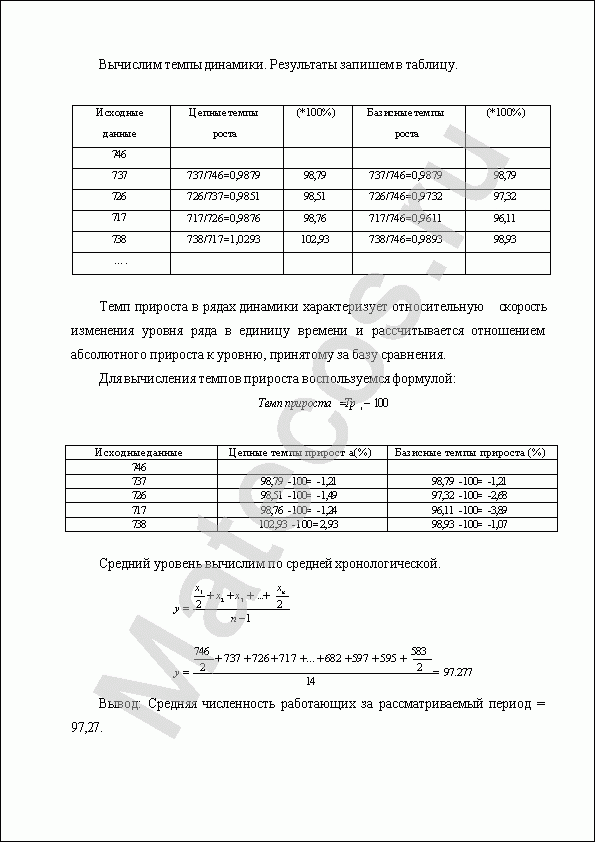
Вычислим темпы динамики. Результаты запишем в таблицу.

Темп прироста в рядах динамики характеризует относительную скорость изменения уровня ряда в единицу времени и рассчитывается отношением абсолютного прироста к уровню, принятому за базу сравнения.
Для вычисления темпов прироста воспользуемся формулой:

Средний уровень вычислим по средней хронологической.

Вывод: Средняя численность работающих за рассматриваемый период = 97,27.

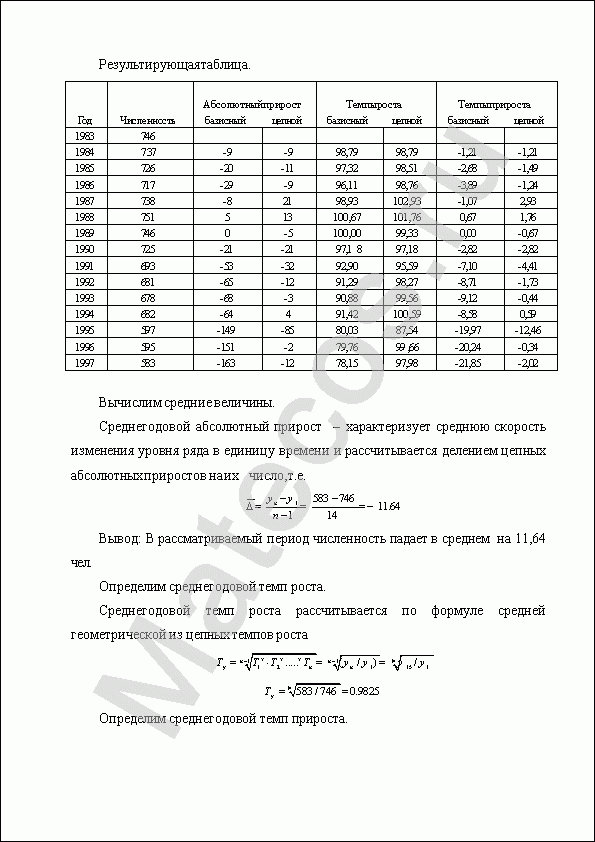
Результирующая таблица.

Вычислим средние величины.
Среднегодовой абсолютный прирост – характеризует среднюю скорость изменения уровня ряда в единицу времени и рассчитывается делением цепных абсолютных приростов на их число, т.е.

Вывод: В рассматриваемый период численность падает в среднем на 11,64 чел.
Определим среднегодовой темп роста.
Среднегодовой темп роста рассчитывается по формуле средней геометрической из цепных темпов роста

Определим среднегодовой темп прироста.

Вывод: За период численность рабочих ежегодно падает на 1,75%

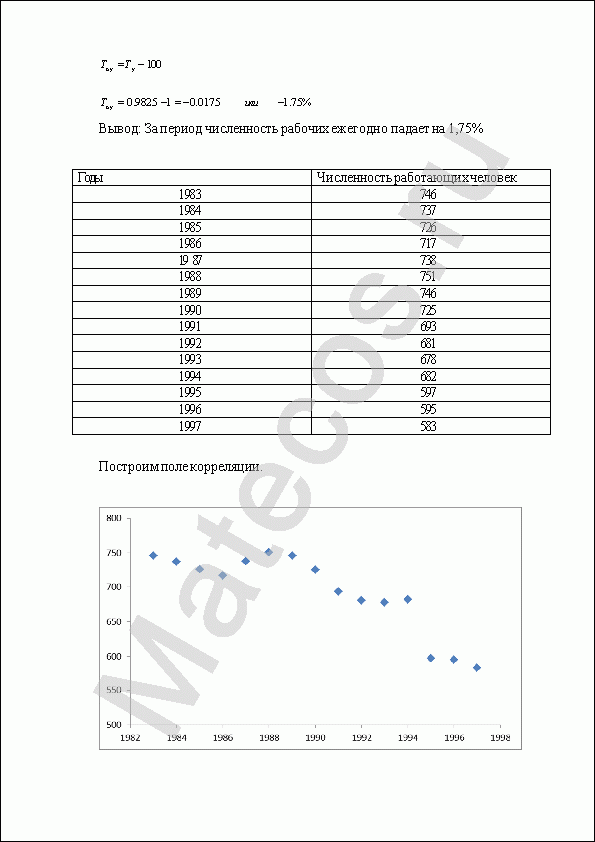
Построим поле корреляции.

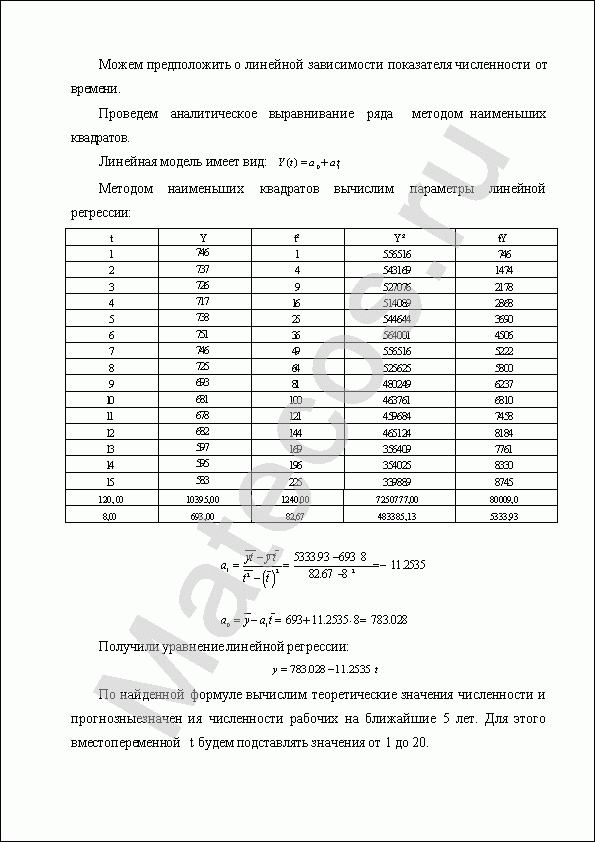
Можем предположить о линейной зависимости показателя численности от времени.
Проведем аналитическое выравнивание ряда методом наименьших квадратов.
Линейная модель имеет вид:
Методом наименьших квадратов вычислим параметры линейной регрессии:

Получили уравнение линейной регрессии:

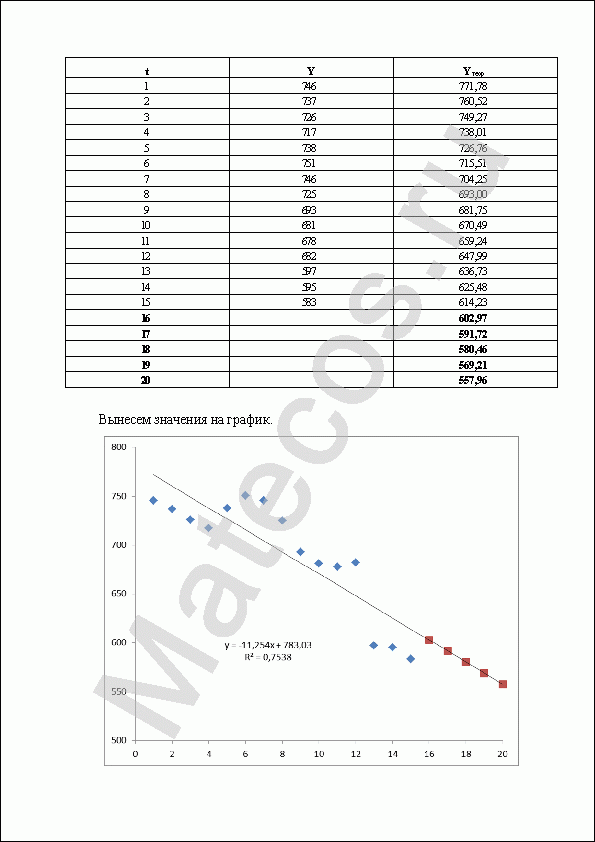
По найденной формуле вычислим теоретические значения численности и прогнозные значения численности рабочих на ближайшие 5 лет. Для этого вместо переменной t будем подставлять значения от 1 до 20.

Вынесем значения на график.