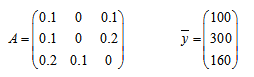ذ’ذ°ر€ذ¸ذ°ذ½ر‚: 4
ذڑذ¾ذ»ذ¸ر‡ذµرپر‚ذ²ذ¾ ذ·ذ°ذ´ذ°ذ½ذ¸ذ¹ / ذ؛ذ¾ذ»ذ¸ر‡ذµرپر‚ذ²ذ¾ رپر‚ر€ذ°ذ½ذ¸ر†: 6 / 28
|
|
ذ—ذ°ذ´ذ°ر‡ذ° 1
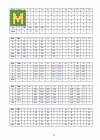
ذ ذ°رپرپذ¼ذ¾ر‚ر€ذ¸ذ¼ ر‚ر€ذ¸ ذ¾ر‚ر€ذ°رپذ»ذ¸ ذ؟ر€ذ¾ذ¼ر‹رˆذ»ذµذ½ذ½ذ¾رپر‚ذ¸: I, II, III, ذ؛ذ°ذ¶ذ´ذ°رڈ ذ¸ذ· ذ؛ذ¾ر‚ذ¾ر€ر‹ر… ذ؟ر€ذ¾ذ¸ذ·ذ²ذ¾ذ´ذ¸ر‚ رپذ²ذ¾ذ¹ ذ¾ذ´ذ½ذ¾ر€ذ¾ذ´ذ½ر‹ذ¹ ذ؟ر€ذ¾ذ´رƒذ؛ر‚ ذ¸ ذ´ذ»رڈ ذ¾ذ±ذµرپذ؟ذµر‡ذµذ½ذ¸رڈ ذ؟ر€ذ¾ذ¸ذ·ذ²ذ¾ذ´رپر‚ذ²ذ° ذ½رƒذ¶ذ´ذ°ذµر‚رپرڈ ذ² ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸ ذ´ر€رƒذ³ذ¸ر… ذ¾ر‚ر€ذ°رپذ»ذµذ¹. ذںر€ذ¾ر†ذµرپرپ ذ؟ر€ذ¾ذ¸ذ·ذ²ذ¾ذ´رپر‚ذ²ذ° ر€ذ°رپرپذ¼ذ°ر‚ر€ذ¸ذ²ذ°ذµر‚رپرڈ ذ·ذ° ذ¾ذ؟ر€ذµذ´ذµذ»ذµذ½ذ½ر‹ذ¹ ذ؟ذµر€ذ¸ذ¾ذ´ ذ²ر€ذµذ¼ذµذ½ذ¸ (ذ½ذ°ذ؟ر€ذ¸ذ¼ذµر€, ذ·ذ° ذ³ذ¾ذ´). ذ’ذ·ذ°ذ¸ذ¼ذ¾ذ´ذµذ¹رپر‚ذ²ذ¸ذµ ذ¾ر‚ر€ذ°رپذ»ذµذ¹ ذ¾ذ؟ر€ذµذ´ذµذ»رڈذµر‚رپرڈ ذ¼ذ°ر‚ر€ذ¸ر†ذµذ¹ ذگ ذ؟ر€رڈذ¼ر‹ر… ذ·ذ°ر‚ر€ذ°ر‚.
ذ§ذ¸رپذ»ذ¾ ذ°ij, رپر‚ذ¾رڈر‰ذµذµ ذ½ذ° ذ؟ذµر€ذµرپذµر‡ذµذ½ذ¸ذ¸ i-ذ¹ رپر‚ر€ذ¾ذ؛ذ¸ ذ¸ j-ذ³ذ¾ رپر‚ذ¾ذ»ذ±ر†ذ°, ر€ذ°ذ²ذ½ذ¾ xij/xj,
ذ³ذ´ذµ
xij – ذ؟ذ¾ر‚ذ¾ذ؛ رپر€ذµذ´رپر‚ذ² ذ؟ر€ذ¾ذ¸ذ·ذ²ذ¾ذ´رپر‚ذ²ذ° ذ¸ذ· i-ذ¹ ذ¾ر‚ر€ذ°رپذ»ذ¸ ذ² j-رژ,
xj – ذ²ذ°ذ»ذ¾ذ²ذ¾ذ¹ ذ¾ذ±رٹذµذ¼ ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸ j-ذ¹ ذ¾ر‚ر€ذ°رپذ»ذ¸ (ذ²رپذµ ذ¾ذ±رٹذµذ¼ر‹ ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸ ذ²ر‹ر€ذ°ذ¶ذ°رژر‚رپرڈ ذ² ذµذ´ذ¸ذ½ذ¸ر†ذ°ر… رپر‚ذ¾ذ¸ذ¼ذ¾رپر‚ذ¸).
ذ—ذ°ذ´ذ°ذ½ ذ²ذµذ؛ر‚ذ¾ر€ ذ¾ذ±رٹذµذ¼ذ¾ذ² ذ؟ر€ذ¾ذ´رƒذ؛ر‚ذ¾ذ² ذ؛ذ¾ذ½ذµر‡ذ½ذ¾ذ³ذ¾ ذ؟ذ¾ر‚ر€ذµذ±ذ»ذµذ½ذ¸رڈ.
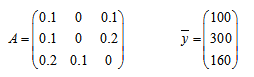
- ذ¾ذ؟ر€ذµذ´ذµذ»ذ¸ر‚رŒ, رڈذ²ذ»رڈذµر‚رپرڈ ذ»ذ¸ ذ¼ذ°ر‚ر€ذ¸ر†ذ° ذگ ذ؟ر€ذ¾ذ´رƒذ؛ر‚ذ¸ذ²ذ½ذ¾ذ¹;
- رپذ¾رپر‚ذ°ذ²ذ¸ر‚رŒ رƒر€ذ°ذ²ذ½ذµذ½ذ¸ذµ ذ¼ذµذ¶ذ¾ر‚ر€ذ°رپذ»ذµذ²ذ¾ذ³ذ¾ ذ±ذ°ذ»ذ°ذ½رپذ°;
- ذ½ذ°ذ¹ر‚ذ¸ ذ¾ذ±رٹذµذ¼ر‹ ذ²ذ°ذ»ذ¾ذ²ذ¾ذ¹ ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸ ذ؛ذ°ذ¶ذ´ذ¾ذ¹ ذ¾ر‚ر€ذ°رپذ»ذ¸ .
- رپذ¾رپر‚ذ°ذ²ذ¸ر‚رŒ ذ¼ذ°ر‚ر€ذ¸ر†رƒ ذ؟ذ¾ر‚ذ¾ذ؛ذ¾ذ² رپر€ذµذ´رپر‚ذ² ذ؟ر€ذ¾ذ¸ذ·ذ²ذ¾ذ´رپر‚ذ²ذ° (xij);
- ذ½ذ°ذ¹ر‚ذ¸ ذ¾ذ±رٹذµذ¼ر‹ ذ²ذ°ذ»ذ¾ذ²ذ¾ذ³ذ¾ ذ²ر‹ذ؟رƒرپذ؛ذ° ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸, ذµرپذ»ذ¸ ذ؛ذ¾ذ½ذµر‡ذ½ذ¾ذµ ذ؟ذ¾ر‚ر€ذµذ±ذ»ذµذ½ذ¸ذµ ذ؟ذ¾ ذ¾ر‚ر€ذ°رپذ»رڈذ¼ رƒذ²ذµذ»ذ¸ر‡ذ¸ر‚رپرڈ ذ½ذ° 60, 70, 30 رپذ¾ذ¾ر‚ذ²ذµر‚رپر‚ذ²ذµذ½ذ½ذ¾.
ذ—ذ°ذ´ذ°ر‡ذ° 2
ذر€ذ³ذ°ذ½ذ¸ذ·ذ°ر†ذ¸ذ¸, ذ·ذ°ذ½ذ¸ذ¼ذ°رژر‰ذµذ¹رپرڈ ذ؟ذµر€ذµذ²ذ¾ذ·ذ؛ذ¾ذ¹ ذ¸ ذ؟ر€ذ¾ذ´ذ°ذ¶ذµذ¹ ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸, ذ½ذµذ¾ذ±ر…ذ¾ذ´ذ¸ذ¼ذ¾ ذ؟ذµر€ذµذ²ذµذ·ر‚ذ¸ ذ؟ذ°ر€ر‚ذ¸رژ ر‚ذ¾ذ²ذ°ر€ذ°. ذںر€ذ¸ رچر‚ذ¾ذ¼ ذ¼ذ¾ذ¶ذ½ذ¾ ذ°ر€ذµذ½ذ´ذ¾ذ²ذ°ر‚رŒ ذ´ذ»رڈ ذ؟ذµر€ذµذ²ذ¾ذ·ذ؛ذ¸ ذ؟ذ¾ ذ¶ذµذ»ذµذ·ذ½ذ¾ذ¹ ذ´ذ¾ر€ذ¾ذ³ذµ 5- ذ¸ 7-ر‚ذ¾ذ½ذ½ر‹ذµ ذ؛ذ¾ذ½ر‚ذµذ¹ذ½ذµر€ر‹. ذںرڈر‚ذ¸ر‚ذ¾ذ½ذ½ر‹ر… ذ؛ذ¾ذ½ر‚ذµذ¹ذ½ذµر€ذ¾ذ² ذ¸ذ¼ذµذµر‚رپرڈ ذ² ذ½ذ°ذ»ذ¸ر‡ذ¸ذ¸ ذ½ذµ ذ±ذ¾ذ»ذµذµ 12 رˆر‚رƒذ؛, ذ° رپذµذ¼ذ¸ ر‚ذ¾ذ½ذ½ر‹ر… – ذ½ذµ ذ±ذ¾ذ»ذµذµ 33 رˆر‚رƒذ؛. ذذ° ذ؟ذµر€ذµذ²ذ¾ذ·ذ؛رƒ ذ²رپذµذ¹ ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸ ذ؟ذ¾ رپذ¼ذµر‚ذµ ذ²ر‹ذ´ذµذ»ذµذ½ذ¾ ذ½ذµ ذ±ذ¾ذ»ذµذµ 120 ر‚ر‹رپرڈر‡ ر€رƒذ±ذ»ذµذ¹, ذ؟ر€ذ¸ر‡ذµذ¼ ر†ذµذ½ذ° ذ·ذ° ذ°ر€ذµذ½ذ´رƒ ذ؟رڈر‚ذ¸ر‚ذ¾ذ½ذ½ذ¾ذ³ذ¾ ذ؛ذ¾ذ½ر‚ذµذ¹ذ½ذµر€ذ° – 2 ر‚ر‹رپ. ر€رƒذ±ذ»ذµذ¹, ذ° رپذµذ¼ذ¸ ر‚ذ¾ذ½ذ½ذ¾ذ³ذ¾ – 3 ر‚ر‹رپ. ر€رƒذ±ذ»ذµذ¹. ذذ؟ر€ذµذ´ذµذ»ذ¸ر‚رŒ, رپذ؛ذ¾ذ»رŒذ؛ذ¾ ذ¸ ذ؛ذ°ذ؛ذ¸ر… ذ؛ذ¾ذ½ر‚ذµذ¹ذ½ذµر€ذ¾ذ² رپذ»ذµذ´رƒذµر‚ ذ°ر€ذµذ½ذ´ذ¾ذ²ذ°ر‚رŒ, ر‡ر‚ذ¾ذ±ر‹ ذ¾ذ±ر‰ذ¸ذ¹ ذ¾ذ±رٹذµذ¼ ذ³ر€رƒذ·ذ¾ذ؟ذµر€ذµذ²ذ¾ذ·ذ¾ذ؛ ذ±ر‹ذ» ذ¼ذ°ذ؛رپذ¸ذ¼ذ°ذ»رŒذ½ر‹ذ¼.
ذ ذµرˆذµذ½ذ¸ذµ ذ·ذ°ذ´ذ°ر‡ذ¸ ذ¾ر„ذ¾ر€ذ¼ذ¸ر‚رŒ ذ؟ذ¾رچر‚ذ°ذ؟ذ½ذ¾:
- ذ؟ذ¾رپر‚ر€ذ¾ذ¸ر‚رŒ ذ¼ذ°ر‚ذµذ¼ذ°ر‚ذ¸ر‡ذµرپذ؛رƒرژ ذ¼ذ¾ذ´ذµذ»رŒ ذ·ذ°ذ´ذ°ر‡ذ¸;
- ر€ذµرˆذ¸ر‚رŒ ذ·ذ°ذ´ذ°ر‡رƒ ذ»ذ¸ذ½ذµذ¹ذ½ذ¾ذ³ذ¾ ذ؟ر€ذ¾ذ³ر€ذ°ذ¼ذ¼ذ¸ر€ذ¾ذ²ذ°ذ½ذ¸رڈ رپ ذ¸رپذ؟ذ¾ذ»رŒذ·ذ¾ذ²ذ°ذ½ذ¸ذµذ¼ ذ³ر€ذ°ر„ذ¸ر‡ذµرپذ؛ذ¾ذ³ذ¾ ذ¼ذµر‚ذ¾ذ´ذ°.
ذ—ذ°ذ´ذ°ر‡ذ° 3
ذذµذ؛ذ¾ر‚ذ¾ر€ذ°رڈ ر„ذ¸ر€ذ¼ذ° ذ²ر‹ذ؟رƒرپذ؛ذ°ذµر‚ ر‡ذµر‚ر‹ر€ذµ ذ²ذ¸ذ´ذ° ر€ذ°ذ·ذ»ذ¸ر‡ذ½ذ¾ذ¹ ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸, ذ¸رپذ؟ذ¾ذ»رŒذ·رƒرڈ ر‡ذµر‚ر‹ر€ذµ ذ²ذ¸ذ´ذ° رپر‹ر€رŒرڈ. ذ’ ر‚ذ°ذ±ذ»ذ¸ر†ذµ رƒذ؛ذ°ذ·ذ°ذ½ر‹:
- ر‚ذµر…ذ½ذ¾ذ»ذ¾ذ³ذ¸ر‡ذµرپذ؛ذ¸ذµ ذ؛ذ¾رچر„ر„ذ¸ر†ذ¸ذµذ½ر‚ر‹ ذ°ij, ذ؛ذ¾ر‚ذ¾ر€ر‹ذµ ذ؟ذ¾ذ؛ذ°ذ·ر‹ذ²ذ°رژر‚, رپذ؛ذ¾ذ»رŒذ؛ذ¾ ذµذ´ذ¸ذ½ذ¸ر† i-ذ³ذ¾ ذ²ذ¸ذ´ذ° رپر‹ر€رŒرڈ ر‚ر€ذµذ±رƒذµر‚رپرڈ ذ´ذ»رڈ ذ؟ر€ذ¾ذ¸ذ·ذ²ذ¾ذ´رپر‚ذ²ذ° ذ¾ذ´ذ½ذ¾ذ¹ ذµذ´ذ¸ذ½ذ¸ر†ر‹ j-ذ³ذ¾ ذ²ذ¸ذ´ذ° ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸;
- ذ؟ر€ذ¸ذ±ر‹ذ»رŒ رپj, ذ؟ذ¾ذ»رƒر‡ذ°ذµذ¼ذ°رڈ ذ¾ر‚ ذ؟ر€ذ¾ذ¸ذ·ذ²ذ¾ذ´رپر‚ذ²ذ° j-ذ³ذ¾ ذ²ذ¸ذ´ذ° ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸ (ذ² ذ½ذ¸ذ¶ذ½ذµذ¹ رپر‚ر€ذ¾ذ؛ذµ ر‚ذ°ذ±ذ»ذ¸ر†ر‹);
- ذ·ذ°ذ؟ذ°رپر‹ رپر‹ر€رŒرڈ ذ² ذ؟ذ»ذ°ذ½ذ¸ر€رƒذµذ¼ر‹ذ¹ ذ؟ذµر€ذ¸ذ¾ذ´ (ذ² ر‚ذµر… ذ¶ذµ ذµذ´ذ¸ذ½ذ¸ر†ذ°ر…).
ذ،ذ¾رپر‚ذ°ذ²ذ¸ر‚رŒ ر‚ذ°ذ؛ذ¾ذ¹ ذ؟ذ»ذ°ذ½ ذ²ر‹ذ؟رƒرپذ؛ذ° ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸, ذ؟ر€ذ¸ ذ؛ذ¾ر‚ذ¾ر€ذ¾ذ¼ ذ±رƒذ´ذµر‚ ذ¾ذ±ذµرپذ؟ذµر‡ذµذ½ذ° ذ¼ذ°ذ؛رپذ¸ذ¼ذ°ذ»رŒذ½ذ°رڈ ذ؟ر€ذ¸ذ±ر‹ذ»رŒ.
ذ ذµرˆذµذ½ذ¸ذµ ذ·ذ°ذ´ذ°ر‡ذ¸ ذ¾ر„ذ¾ر€ذ¼ذ¸ر‚رŒ ذ؟ذ¾رچر‚ذ°ذ؟ذ½ذ¾:
- رپذ¾رپر‚ذ°ذ²ذ¸ر‚رŒ ذ¼ذ°ر‚ذµذ¼ذ°ر‚ذ¸ر‡ذµرپذ؛رƒرژ ذ¼ذ¾ذ´ذµذ»رŒ ذ·ذ°ذ´ذ°ر‡ذ¸;
- ذ؟ر€ذ¸ذ²ذµرپر‚ذ¸ ذ·ذ°ذ´ذ°ر‡رƒ ذ؛ ذ؛ذ°ذ½ذ¾ذ½ذ¸ر‡ذµرپذ؛ذ¾ذ¼رƒ ذ²ذ¸ذ´رƒ, ذ؟ذ¾رڈرپذ½ذ¸ر‚رŒ رچذ؛ذ¾ذ½ذ¾ذ¼ذ¸ر‡ذµرپذ؛ذ¸ذ¹ رپذ¼ر‹رپذ» ذ´ذ¾ذ؟ذ¾ذ»ذ½ذ¸ر‚ذµذ»رŒذ½ر‹ر… ذ؟ذµر€ذµذ¼ذµذ½ذ½ر‹ر…;
- ر€ذµرˆذ¸ر‚رŒ ذ·ذ°ذ´ذ°ر‡رƒ رپذ¸ذ¼ذ؟ذ»ذµذ؛رپ-ذ¼ذµر‚ذ¾ذ´ذ¾ذ¼;
- ذ¾ذ؟ر€ذµذ´ذµذ»ذ¸ر‚رŒ ذ؛ذ¾ذ»ذ¸ر‡ذµرپر‚ذ²ذ¾ ذ½ذµذ¸ذ·ر€ذ°رپر…ذ¾ذ´ذ¾ذ²ذ°ذ½ذ½ذ¾ذ³ذ¾ رپر‹ر€رŒرڈ ذ؟ر€ذ¸ ذ½ذ°ذ¹ذ´ذµذ½ذ½ذ¾ذ¼ ذ¾ذ؟ر‚ذ¸ذ¼ذ°ذ»رŒذ½ذ¾ذ¼ ذ؟ذ»ذ°ذ½ذµ;
- ذ؟ذ¾رپر‚ر€ذ¾ذ¸ر‚رŒ ذ´ذ²ذ¾ذ¹رپر‚ذ²ذµذ½ذ½رƒرژ ذ·ذ°ذ´ذ°ر‡رƒ, ر€ذµرˆذ¸ر‚رŒ ذµذµ;
- ذ´ذ°ر‚رŒ رچذ؛ذ¾ذ½ذ¾ذ¼ذ¸ر‡ذµرپذ؛ذ¸ذ¹ ذ°ذ½ذ°ذ»ذ¸ذ· ذ´ذ²ذ¾ذ¹رپر‚ذ²ذµذ½ذ½ذ¾ذ¹ ذ·ذ°ذ´ذ°ر‡ذ¸, ذ¾ر†ذµذ½ذ¸ر‚رŒ ر†ذµذ»ذµرپذ¾ذ¾ذ±ر€ذ°ذ·ذ½ذ¾رپر‚رŒ ذ²ذ²ذµذ´ذµذ½ذ¸رڈ ذ² ذ؟ذ»ذ°ذ½ ذ½ذ¾ذ²ذ¾ذ³ذ¾ ذ²ذ¸ذ´ذ° ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸, ذµرپذ»ذ¸ ذ·ذ°ر‚ر€ذ°ر‚ر‹ ذ½ذ° ذ؟ر€ذ¾ذ¸ذ·ذ²ذ¾ذ´رپر‚ذ²ذ¾ رچر‚ذ¾ذ¹ ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸ ذ¸ ذ؟ذ¾ذ»رƒر‡ذ°ذµذ¼ذ°رڈ ذ؟ر€ذ¸ذ±ر‹ذ»رŒ ذ·ذ°ذ´ذ°ذ½ر‹ ذ² ذ؟ذ¾رپذ»ذµذ´ذ½ذµذ¹ ذ³ر€ذ°ر„ذµ ر‚ذ°ذ±ذ»ذ¸ر†ر‹.
| ذ،ر‹ر€رŒذµ - ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸رڈ |
ذ¢ذµر…ذ½ذ¾ذ»ذ¾ذ³ذ¸ر‡ذµرپذ؛ذ¸ذµ ذ؛ذ¾رچر„ر„ذ¸ر†ذ¸ذµذ½ر‚ر‹ ذ°ij |
ذ—ذ°ذ؟ذ°رپر‹ رپر‹ر€رŒرڈ |
ذذ¾ذ²ر‹ذ¹ ذ²ذ¸ذ´ ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸ذ¸ |
| A |
B |
C |
D |
| I |
2 |
0,5 |
1 |
0,5 |
400 |
0 |
| II |
1 |
2 |
1 |
1,5 |
500 |
1 |
| III |
1 |
1 |
1 |
0,5 |
300 |
3 |
| IV |
1 |
1 |
0 |
1 |
100 |
4 |
| ذںر€ذ¸ذ±ر‹ذ»رŒ رپj |
4 |
5 |
3 |
4 |
|
22 |
ذ—ذ°ذ´ذ°ر‡ذ° 4
ذ’ ذ³ذ¾ر€ذ¾ذ´ذµ ذ¸ذ¼ذµرژر‚رپرڈ ر‚ر€ذ¸ ذ´ذ¾ذ¼ذ¾رپر‚ر€ذ¾ذ¸ر‚ذµذ»رŒذ½ر‹ر… ذ؛ذ¾ذ¼ذ±ذ¸ذ½ذ°ر‚ذ° (ذ”ذ،ذڑ): ذگ1, ذگ2, ذگ3 ذ¸ رپر‚ر€ذ¾رڈر‚رپرڈ ر‡ذµر‚ر‹ر€ذµ ذ¼ذ¸ذ؛ر€ذ¾ر€ذ°ذ¹ذ¾ذ½ذ°: ذ’1, ذ’2, ذ’3, ذ’4. ذکذ·ذ²ذµرپر‚ذ½ر‹ ر€ذµرپرƒر€رپر‹: ذگ1 – 100, ذگ2 – 130, ذگ3 – 170 ذ¸ ذ؟ر€ذ¾ذ¸ذ·ذ²ذ¾ذ´رپر‚ذ²ذµذ½ذ½ر‹ذµ ذ؟ذ¾ر‚ر€ذµذ±ذ½ذ¾رپر‚ذ¸ رƒذ½ذ¸ر„ذ¸ر†ذ¸ر€ذ¾ذ²ذ°ذ½ذ½ر‹ر… ذ¸ذ·ذ´ذµذ»ذ¸ذ¹ ذ¼ذ¸ذ؛ر€ذ¾ر€ذ°ذ¹ذ¾ذ½ذ°: ذ’1 – 150, ذ’2 – 120, ذ’3 – 80, ذ’4 – 50. ذکذ·ذ²ذµرپر‚ذ½ر‹ ر‚ذ°ذ؛ذ¶ذµ ذ·ذ°ر‚ر€ذ°ر‚ر‹, رپذ²رڈذ·ذ°ذ½ذ½ر‹ذµ رپ ذ´ذ¾رپر‚ذ°ذ²ذ؛ذ¾ذ¹ ذ¾ذ´ذ½ذ¾ذ³ذ¾ ذ؛ذ¾ذ¼ذ؟ذ»ذµذ؛ر‚ذ° رƒذ½ذ¸ر„ذ¸ر†ذ¸ر€ذ¾ذ²ذ°ذ½ذ½ر‹ر… ذ¸ذ·ذ´ذµذ»ذ¸ذ¹ ذ¸ذ· ذ؛ذ°ذ¶ذ´ذ¾ذ³ذ¾ ذ؟رƒذ½ذ؛ر‚ذ° ذ؛ذ¾ذ¼ذ؟ذ»ذµذ؛ر‚ذ¾ذ²ذ°ذ½ذ¸رڈ ذ² ذ؛ذ°ذ¶ذ´ر‹ذ¹ ذ؟رƒذ½ذ؛ر‚ ذ½ذ°ذ·ذ½ذ°ر‡ذµذ½ذ¸رڈ.
| |
B1 |
B2 |
B3 |
B4 |
| A1 |
3 |
5 |
7 |
11 |
| A2 |
1 |
4 |
6 |
3 |
| A3 |
5 |
8 |
12 |
7 |
ذ¢ر€ذµذ±رƒذµر‚رپرڈ ر€ذ°رپذ؟ر€ذµذ´ذµذ»ذ¸ر‚رŒ ذ؟ر€ذ¾ذ´رƒذ؛ر†ذ¸رژ ذ”ذ،ذڑ ذ؟ذ¾ ذ¼ذ¸ذ؛ر€ذ¾ر€ذ°ذ¹ذ¾ذ½ذ°ذ¼, ر‡ر‚ذ¾ذ±ر‹ رپرƒذ¼ذ¼ذ°ر€ذ½ر‹ذµ ذ؟ر€ذ¸ذ²ذµذ´ذµذ½ذ½ر‹ذµ ذ·ذ°ر‚ر€ذ°ر‚ر‹, رپذ²رڈذ·ذ°ذ½ذ½ر‹ذµ رپ ذ´ذ¾رپر‚ذ°ذ²ذ؛ذ¾ذ¹ ذ²رپذµذ³ذ¾ ذ³ر€رƒذ·ذ° ذ¾ر‚ ذ¾ر‚ذ؟ر€ذ°ذ²ذ¸ر‚ذµذ»رڈ ذ؛ ذ؟ذ¾ر‚ر€ذµذ±ذ¸ر‚ذµذ»رژ, ذ±ر‹ذ»ذ¸ ذ¼ذ¸ذ½ذ¸ذ¼ذ°ذ»رŒذ½ر‹.
ذ—ذ°ذ´ذ°ر‡ذ° 5
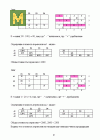
ذ،ذ²ذµرپر‚ذ¸ ذ¼ذ°ر‚ر€ذ¸ر‡ذ½رƒرژ ذ¸ذ³ر€رƒ ذ؛ ذ·ذ°ذ´ذ°ر‡ذµ ذ»ذ¸ذ½ذµذ¹ذ½ذ¾ذ³ذ¾ ذ؟ر€ذ¾ذ³ر€ذ°ذ¼ذ¼ذ¸ر€ذ¾ذ²ذ°ذ½ذ¸رڈ:
| 3 |
1 |
2 |
1 |
3 |
| 8 |
8 |
0 |
7 |
2 |
| 5 |
4 |
8 |
8 |
5 |
ذ—ذ°ذ´ذ°ر‡ذ° 6
ذذ؟ر€ذµذ´ذµذ»ذ¸ر‚ذµ ر‚ذ¸ذ؟ رچذ»ذµذ؛ر‚ر€ذ¾رپر‚ذ°ذ½ر†ذ¸ذ¸, ذ؛ذ¾ر‚ذ¾ر€رƒرژ ذ½ذµذ¾ذ±ر…ذ¾ذ´ذ¸ذ¼ذ¾ ذ؟ذ¾رپر‚ر€ذ¾ذ¸ر‚رŒ ذ´ذ»رڈ رƒذ´ذ¾ذ²ذ»ذµر‚ذ²ذ¾ر€ذµذ½ذ¸رڈ رچذ½ذµر€ذ³ذµر‚ذ¸ر‡ذµرپذ؛ذ¸ر… ذ؟ذ¾ر‚ر€ذµذ±ذ½ذ¾رپر‚ذµذ¹ ذ؛ذ¾ذ¼ذ؟ذ»ذµذ؛رپذ° ذ؛ر€رƒذ؟ذ½ر‹ر… ذ؟ر€ذ¾ذ¼ر‹رˆذ»ذµذ½ذ½ر‹ر… ذ؟ر€ذµذ´ذ؟ر€ذ¸رڈر‚ذ¸ذ¹. ذ’ذ¾ذ·ذ¼ذ¾ذ¶ذ½ر‹ذµ رپر‚ر€ذ°ر‚ذµذ³ذ¸ذ¹ ذ² ذ·ذ°ذ´ذ°ر‡ذµ:
ذگ1 – رپذ¾ذ¾ر€رƒذ¶ذ°ذµر‚رپرڈ ذ³ذ¸ذ´ر€ذ¾رپر‚ذ°ذ½ر†ذ¸رڈ;
ذگ2 – رپذ¾ذ¾ر€رƒذ¶ذ°ذµر‚رپرڈ ر‚ذµذ؟ذ»ذ¾رپر‚ذ°ذ½ر†ذ¸رڈ;
ذگ3 – رپذ¾ذ¾ر€رƒذ¶ذ°ذµر‚رپرڈ ذ°ر‚ذ¾ذ¼ذ½ذ°رڈ رپر‚ذ°ذ½ر†ذ¸رڈ.
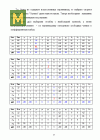
ذذ؛ذ¾ذ½ذ¾ذ¼ذ¸ر‡ذµرپذ؛ذ°رڈ رچر„ر„ذµذ؛ر‚ذ¸ذ²ذ½ذ¾رپر‚رŒ رپذ¾ذ¾ر€رƒذ¶ذµذ½ذ¸رڈ رچذ»ذµذ؛ر‚ر€ذ¾رپر‚ذ°ذ½ر†ذ¸ذ¸ ذ·ذ°ذ²ذ¸رپذ¸ر‚ ذ¾ر‚ ذ²ذ»ذ¸رڈذ½ذ¸رڈ رپذ»رƒر‡ذ°ذ¹ذ½ر‹ر… ر„ذ°ذ؛ر‚ذ¾ر€ذ¾ذ², ذ¾ذ±ر€ذ°ذ·رƒرژر‰ذ¸ر… ذ¼ذ½ذ¾ذ¶ذµرپر‚ذ²ذ¾ رپذ¾رپر‚ذ¾رڈذ½ذ¸ذ¹ ذ؟ر€ذ¸ر€ذ¾ذ´ر‹ ذںi. ذ ذµذ·رƒذ»رŒر‚ذ°ر‚ر‹ ر€ذ°رپر‡ذµر‚ذ° رچذ؛ذ¾ذ½ذ¾ذ¼ذ¸ر‡ذµرپذ؛ذ¾ذ¹ رچر„ر„ذµذ؛ر‚ذ¸ذ²ذ½ذ¾رپر‚ذ¸ ذ؟ر€ذ¸ذ²ذµذ´ذµذ½ر‹ ذ² ر‚ذ°ذ±ذ».
| ذ¢ذ¸ذ؟ رپر‚ذ°ذ½ر†ذ¸ذ¸ |
ذ،ذ¾رپر‚ذ¾رڈذ½ذ¸ذµ ذ؟ر€ذ¸ر€ذ¾ذ´ر‹ |
| ذں1 |
ذں2 |
ذں3 |
ذں4 |
ذں5 |
| ذگ1 |
40 |
70 |
30 |
25 |
45 |
| ذگ2 |
60 |
50 |
45 |
20 |
30 |
| ذگ3 |
50 |
30 |
40 |
35 |
60 |
ذکرپذ؟ذ¾ذ»رŒذ·ذ¾ذ²ذ°ر‚رŒ ذ؛ر€ذ¸ر‚ذµر€ذ¸ذ¸ ذ’ذ°ذ»رŒذ´ذ°, ذ،رچذ²ذ¸ذ´ذ¶ذ° ذ¸ ذ“رƒر€ذ²ذ¸ر†ذ° ذ´ذ»رڈ خ» = 0.3. ذ،ر€ذ°ذ²ذ½ذ¸ر‚رŒ ر€ذµرˆذµذ½ذ¸رڈ ذ¸ رپذ´ذµذ»ذ°ر‚رŒ ذ²ر‹ذ²ذ¾ذ´.