Математические методы в экономике - готовые контрольные (27)
Тут Вы можете заказать контрольную работу по методам и моделям в экономике без предоплаты
Вариант: 4Количество заданий / количество страниц: 6 / 28 |
Отправить также файл на почту |
Задача 1
Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат.
Число аij, стоящее на пересечении i-й строки и j-го столбца, равно xij/xj,
где
xij – поток средств производства из i-й отрасли в j-ю,
xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости).
Задан вектор объемов продуктов конечного потребления.
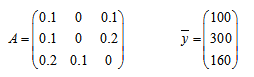
- определить, является ли матрица А продуктивной;
- составить уравнение межотраслевого баланса;
- найти объемы валовой продукции каждой отрасли .
- составить матрицу потоков средств производства (xij);
- найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
Задача 2
Организации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 12 штук, а семи тонных – не более 33 штук. На перевозку всей продукции по смете выделено не более 120 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семи тонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
- построить математическую модель задачи;
- решить задачу линейного программирования с использованием графического метода.
Задача 3
Некоторая фирма выпускает четыре вида различной продукции, используя четыре вида сырья. В таблице указаны:
- технологические коэффициенты аij, которые показывают, сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
- прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
- запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
- составить математическую модель задачи;
- привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
- решить задачу симплекс-методом;
- определить количество неизрасходованного сырья при найденном оптимальном плане;
- построить двойственную задачу, решить ее;
- дать экономический анализ двойственной задачи, оценить целесообразность введения в план нового вида продукции, если затраты на производство этой продукции и получаемая прибыль заданы в последней графе таблицы.
| Сырье - продукция | Технологические коэффициенты аij | Запасы сырья | Новый вид продукции | |||
| A | B | C | D | |||
| I | 2 | 0,5 | 1 | 0,5 | 400 | 0 |
| II | 1 | 2 | 1 | 1,5 | 500 | 1 |
| III | 1 | 1 | 1 | 0,5 | 300 | 3 |
| IV | 1 | 1 | 0 | 1 | 100 | 4 |
| Прибыль сj | 4 | 5 | 3 | 4 | 22 | |
Задача 4
В городе имеются три домостроительных комбината (ДСК): А1, А2, А3 и строятся четыре микрорайона: В1, В2, В3, В4. Известны ресурсы: А1 – 100, А2 – 130, А3 – 170 и производственные потребности унифицированных изделий микрорайона: В1 – 150, В2 – 120, В3 – 80, В4 – 50. Известны также затраты, связанные с доставкой одного комплекта унифицированных изделий из каждого пункта комплектования в каждый пункт назначения.
| B1 | B2 | B3 | B4 | |
| A1 | 3 | 5 | 7 | 11 |
| A2 | 1 | 4 | 6 | 3 |
| A3 | 5 | 8 | 12 | 7 |
Требуется распределить продукцию ДСК по микрорайонам, чтобы суммарные приведенные затраты, связанные с доставкой всего груза от отправителя к потребителю, были минимальны.
Задача 5
Свести матричную игру к задаче линейного программирования:
| 3 | 1 | 2 | 1 | 3 |
| 8 | 8 | 0 | 7 | 2 |
| 5 | 4 | 8 | 8 | 5 |
Задача 6
Определите тип электростанции, которую необходимо построить для удовлетворения энергетических потребностей комплекса крупных промышленных предприятий. Возможные стратегий в задаче:
А1 – сооружается гидростанция;
А2 – сооружается теплостанция;
А3 – сооружается атомная станция.
Экономическая эффективность сооружения электростанции зависит от влияния случайных факторов, образующих множество состояний природы Пi. Результаты расчета экономической эффективности приведены в табл.
| Тип станции | Состояние природы | ||||
| П1 | П2 | П3 | П4 | П5 | |
| А1 | 40 | 70 | 30 | 25 | 45 |
| А2 | 60 | 50 | 45 | 20 | 30 |
| А3 | 50 | 30 | 40 | 35 | 60 |