Графики функций. Простейшие построения. Прямая на плоскости

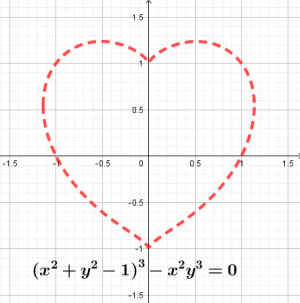График функции - это наглядный образ некоторой функции f(x). Здесь каждому значению х соответствует единственное значение y. Это множество точек на плоскости, координаты которых удовлетворяют заданному уравнению y = f(x). График уравнения - это множество всех точек плоскости, которые удовлетворяют заданному уравнению, т.е. обращают уравнение в верное числовое равенство. Зависимость в данном случае не обязательно является функцией. Рассмотрим ряд элементарных функций, таких, как прямая, парабола, гипербола, их свойства и правила построения.

Но для начала покажем на примере отличие графика функции от графика уравнения.

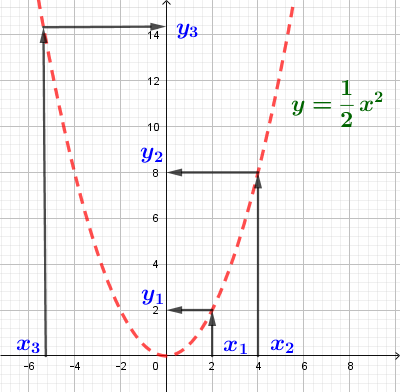
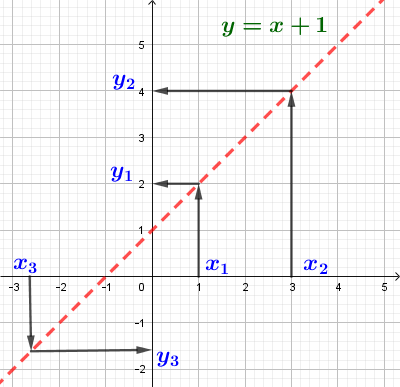
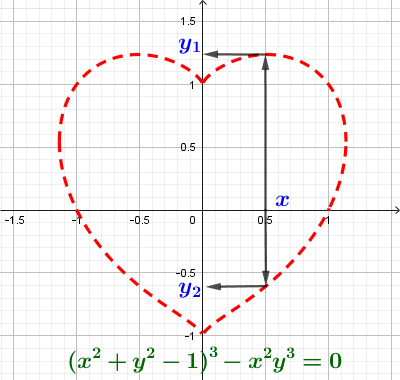
1. Прямая. Уравнение прямой y = kx + b.

Прямая задается линейной функцией , т.е. уравнением первой степени вида y = kx + b.

при k>0 график функции возрастает (y=3x+1, k=3, k>0), при k<0 график функции убывает (y=-3x+1, k=-3, k<0)

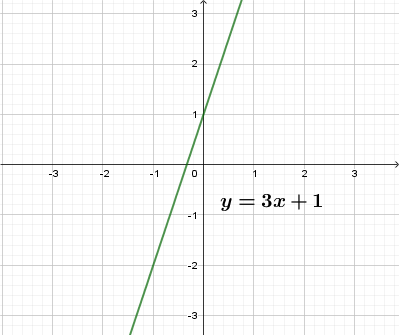
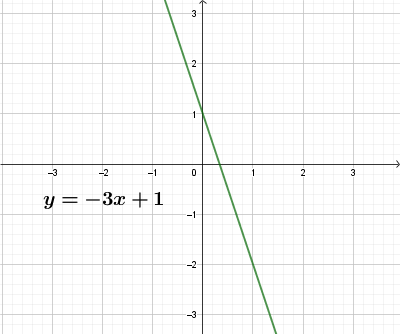
Рассмотрим частные случаи расположения линейных функций.

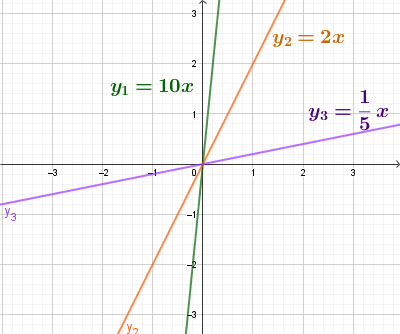
y = kx - график функции проходит через начало координат, т.е. точку О(0;0),

y = c (c = const) - график функции параллелен оси Ox,

x = c (c = const) - график функции параллелен оси Oy.

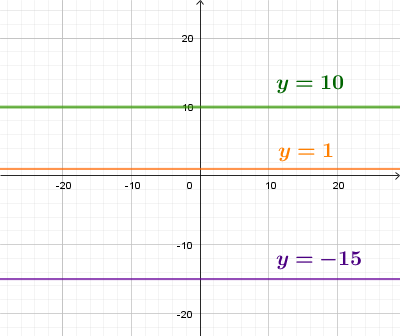
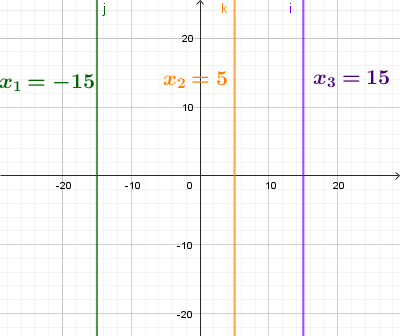
Для построения прямой достаточно получить координаты двух точек, принадлежащих заданному уравнению. 

Как построить прямую? Покажем на примере.

Дано уравнение прямой: y=-2x+3. Необходимо построить график функции.

Возьмем два произвольных значения переменной х, например х = -1 и х = 5. Найдем для каждого из них соответствующее значение переменной у. Как это сделать? Подставить выбранные значения х в заданное уравнение.

y(-1) = -2·(-1)+3=5

y(5) = -2·5+3=-7

Получаем две точки с координатами: (-1;5) и (5;-7). Выносим их на координатную плоскость и проводим через них прямую.

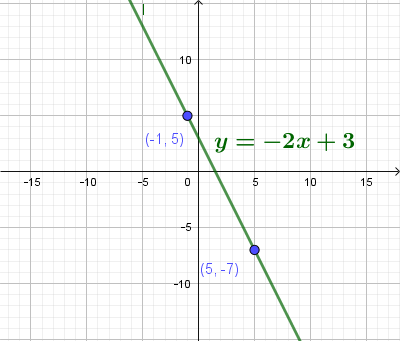
На что указывают параметры k,b в уравнении прямой y = kx + b?

Параметр k - указывает на наклон прямой.

Параметр b - координата точки пересечения заданной прямой с осью OY. Так как y = k·0 + b (х=0 - уравнение оси OY)

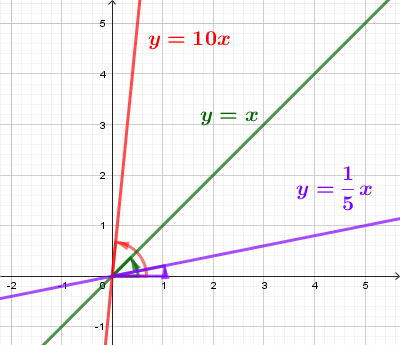
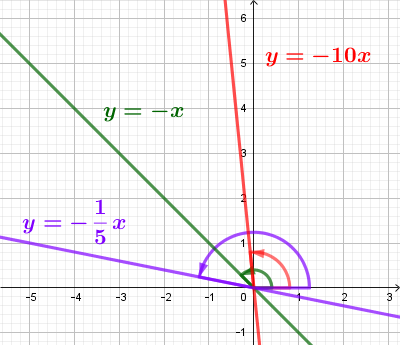
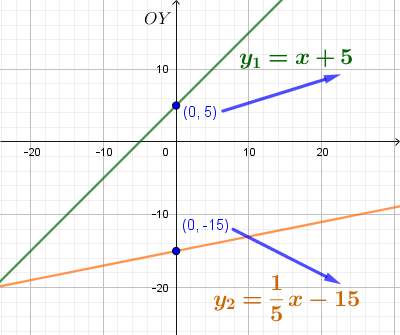
Параметр k в уравнении прямой y = kx + b есть угловой коэффициент этой прямой.

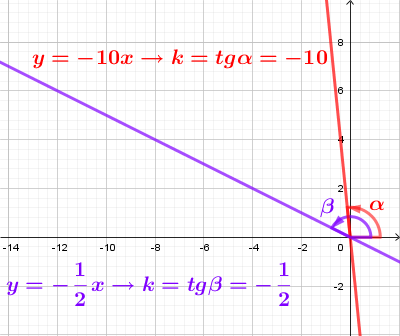
k=tgα, α - угол меду положительным направлением оси ОХ и прямой.

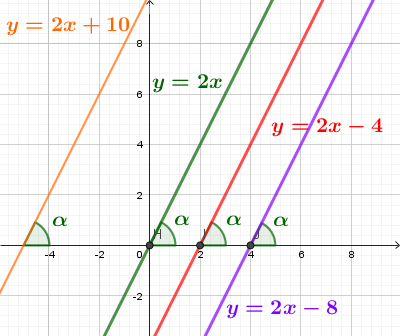
Угловые коэффициенты всех параллельных прямых равны.

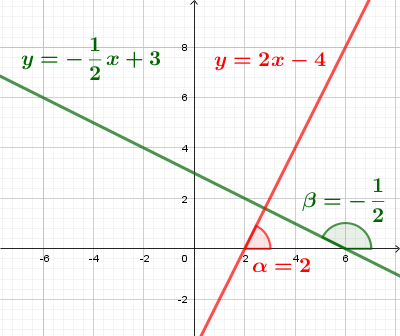
Угловые коэффициенты перпендикулярных прямых взаимно обратны по величине и противоположны по знаку.

Для наглядности покажем утверждения на конкретных примерах.

Уравнения прямой на плоскости.

Построим некоторые уравнения прямых в зависимости от исходных данных, приведем формулы и рассмотрим конкретные примеры.

Коротко уточним используемые ниже понятия:

Угол наклона прямой - угол меду положительным направлением оси ОХ и прямой.

Нормальный вектор прямой - вектор, перпендикулярный искомой прямой.

Направляющий вектор прямой - вектор, параллельный искомой прямой.