Преобразование графиков функции
В данном разделе рассмотрим всевозможные геометрические преобразования графиков. Вы убедитесь, что все просто и не будете более пугаться вида "страшной" функции, график которой Вам предстоит построить.
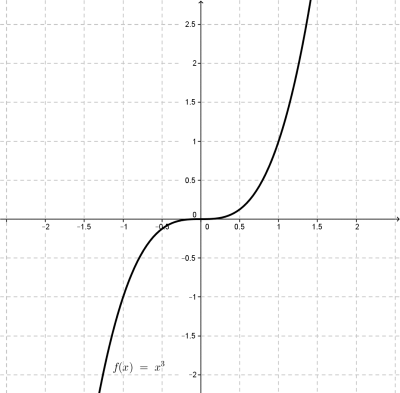
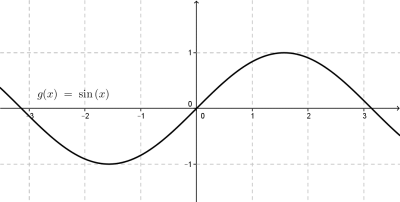
Все "эксперименты" будем производить с кубической параболои f=x3 и синусоидой g=sin(x)
 |
 |
Поскольку мы решили заняться математикй, а это наука точная, то помимо доступно-художественного описания произведенных действий будем прилагать некоторые математические термины.
Преобразование 1: y = f(x) + a
Рассмотрим на примере кубической параболы и синусоиды:
f1 = x3 + 2
g1 = sin(x) - 3 или g1 = sin(x) + (-3)
В обоих случаях к исходным функциям прибавляют или вычитают некоторое число а.
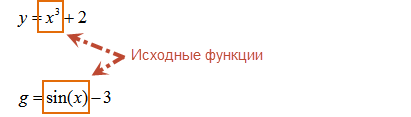
Что происходит с графиком функции?
Исходный график функции перемещается вверх на а единиц, если а положительно; перемещается вниз, при а отрицательном.
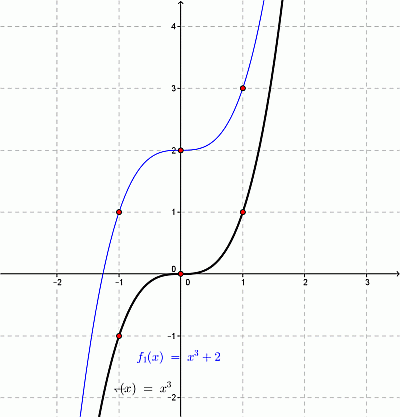 или
или 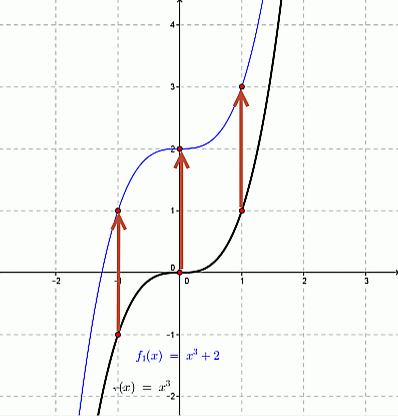
Для более точного переноса, взяли на графике некоторые точки и подняли их на 2 единицы (клетки) вверх. По этим точкам провели построение.
Пример 1
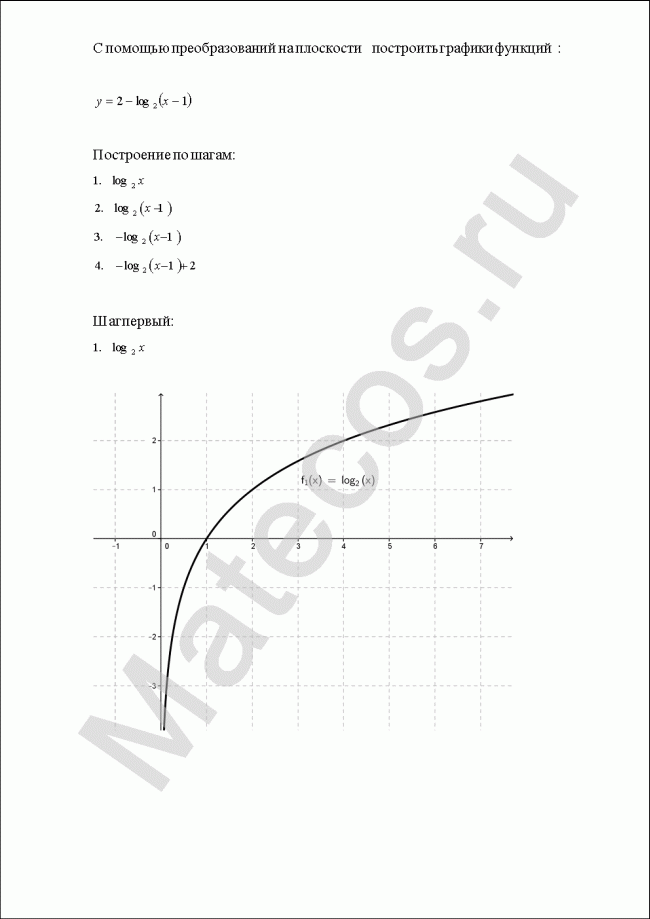
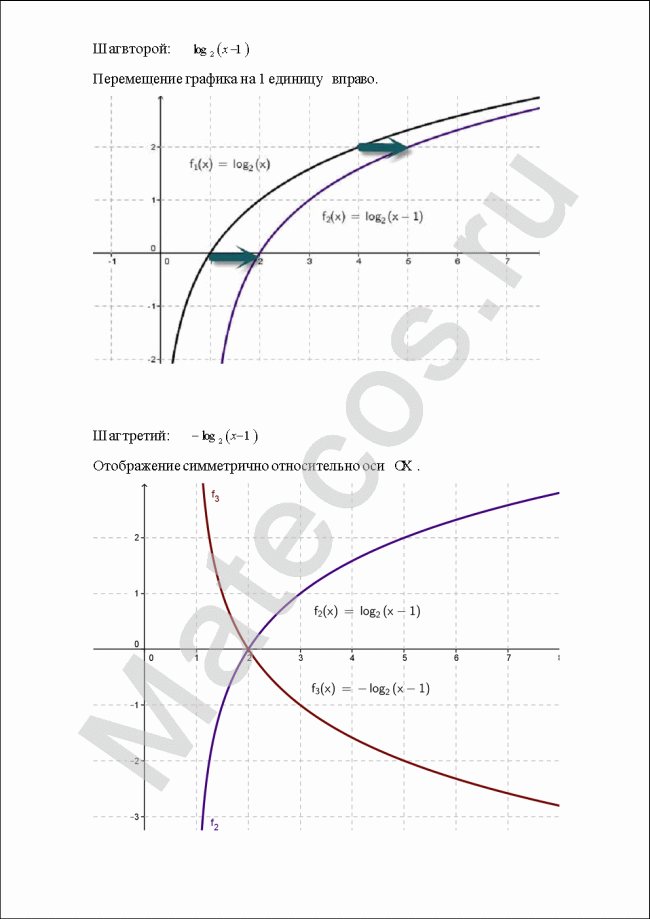
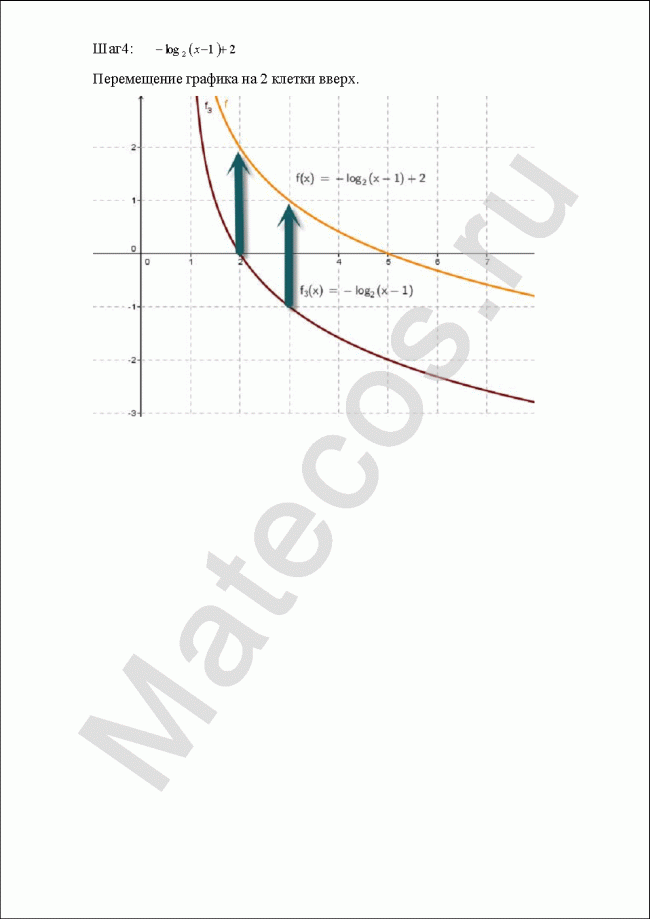
С помощью преобразований на плоскости построить графики функций:
![]()
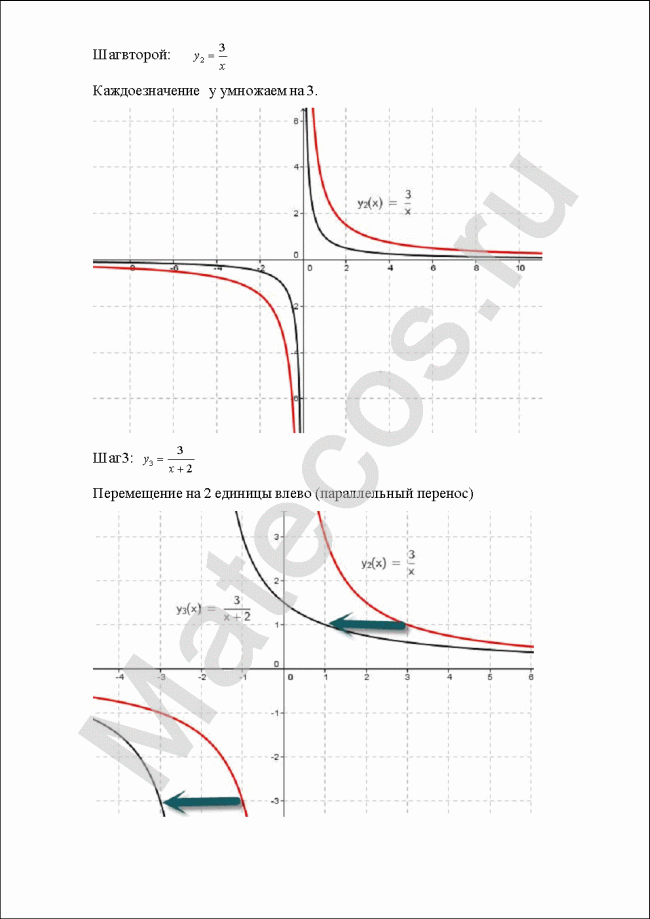
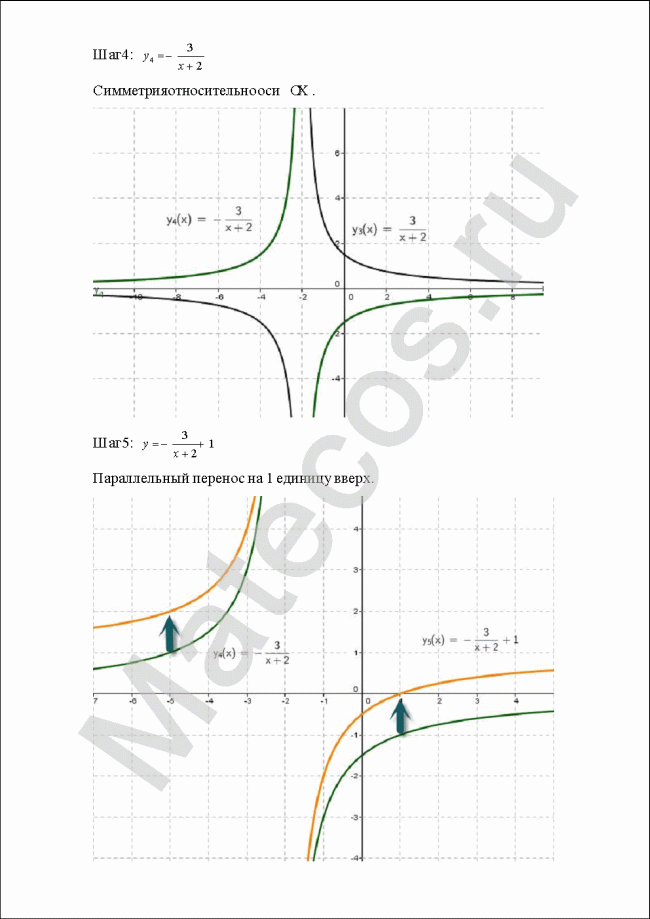
Пример 2
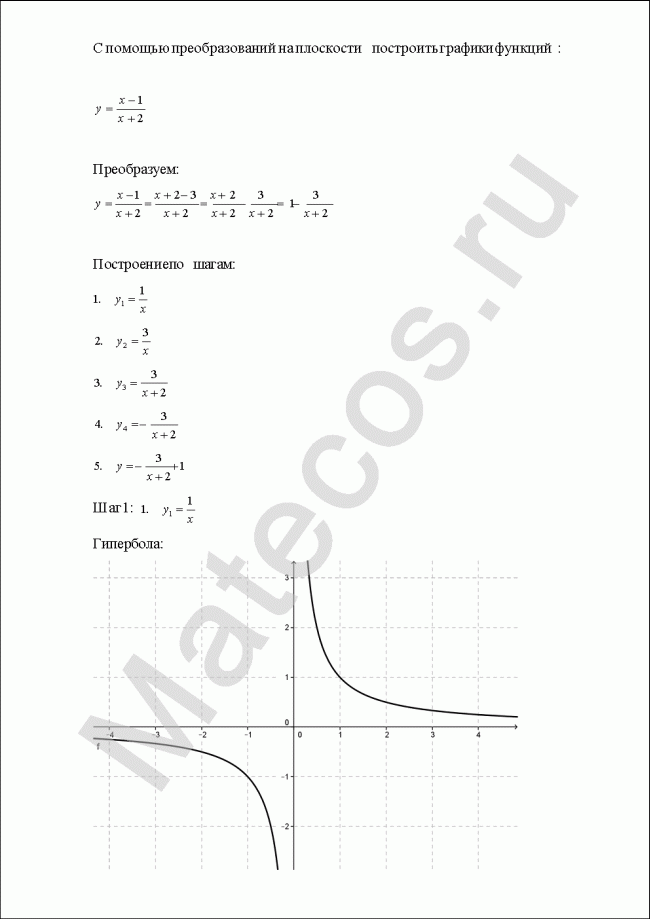
С помощью преобразований на плоскости построить графики функций:
![]()
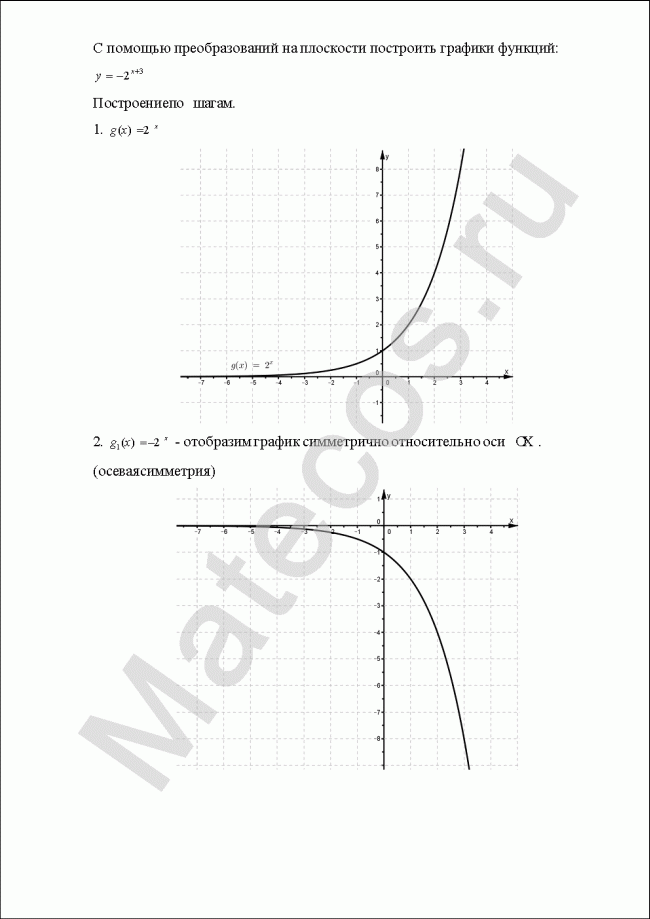
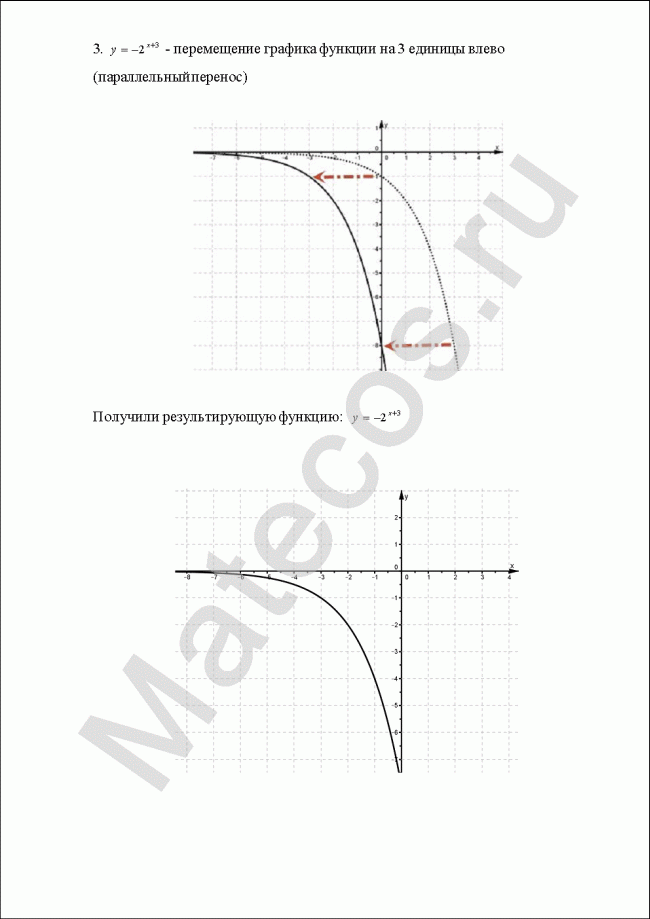
Пример 3
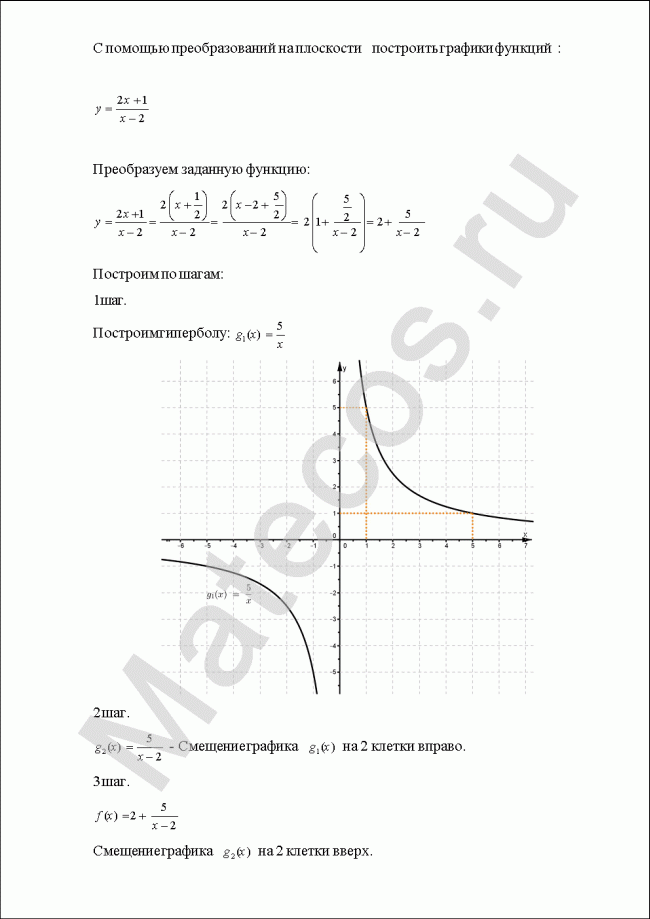
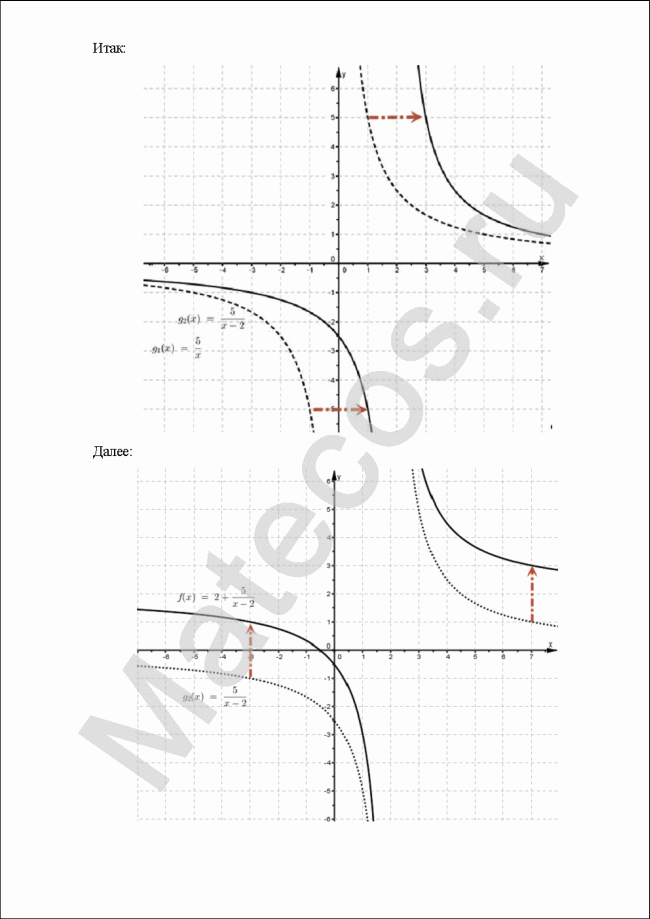
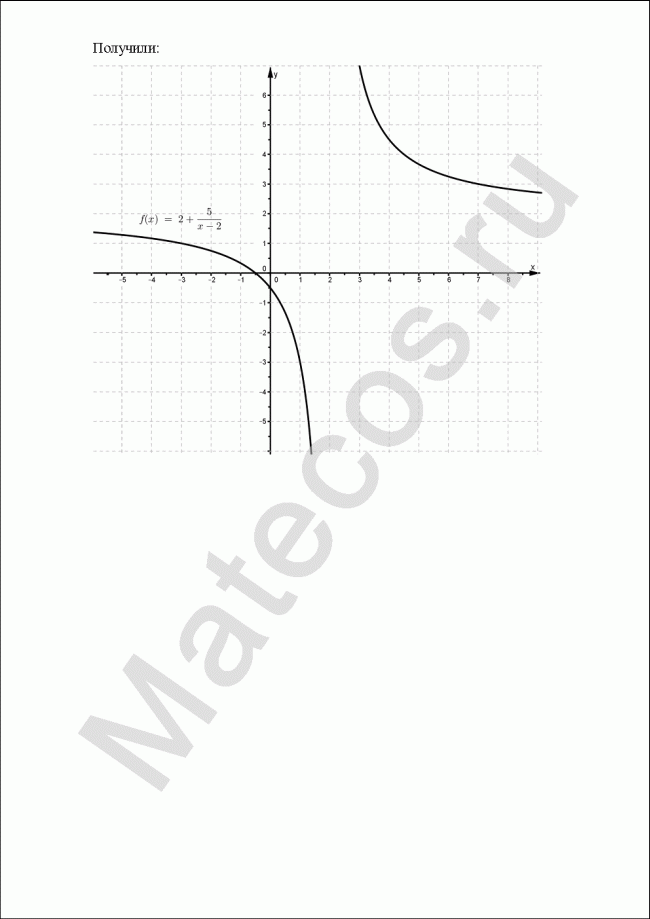
С помощью преобразований на плоскости построить графики функций:
![]()
Пример 4
С помощью преобразований на плоскости построить графики функций:
![]()