Вариант 01: номер рисунка 0, номер условия 1
Теоретическая механика делится на три раздела: С-статика, К-кинематика, Д-динамика. Номер варианта выбирается по двум последним цифрам зачетной книжки: первая цифра - номер рисунка, вторая - номер условия задачи.
Решение задачи по термеху С1-01 методичка Тарг 1988
Отправить также файл на почту |
Отправить также файл на почту |
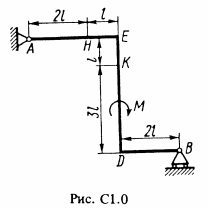
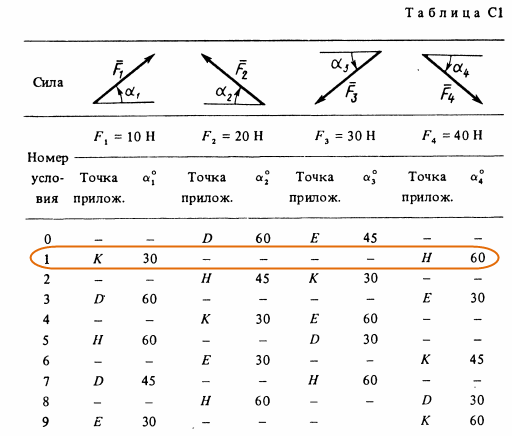
Жесткая рама, расположенная в вертикальной плоскости (рис. С1.0 — С1.9, табл. С1), закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню ВВ1, или к шарнирной опоре на катках; стержень прикреплен к раме и к неподвижной опоре шарнирами. На раму действуют пара сил с моментом М = 100 кН·м и две силы, значения, направления и точки приложения которых указаны в таблице (например, в условиях № 1 на раму действует сила F1 = 10 Н под углом 30° к горизонтальной оси, приложенная в точке K и сила F4 = 40 Н под углом 60° к горизонтальной оси, приложенная в точке H, и т. д.). Определить реакции связей в точках A, В, вызываемые заданными нагрузками. При окончательных расчетах принять l = 0,5 м.
 |
 |
Решение задачи по термеху С2-01 методичка Тарг 1988
Отправить также файл на почту |
Отправить также файл на почту |
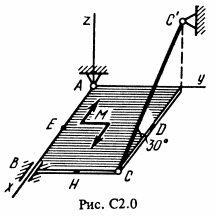
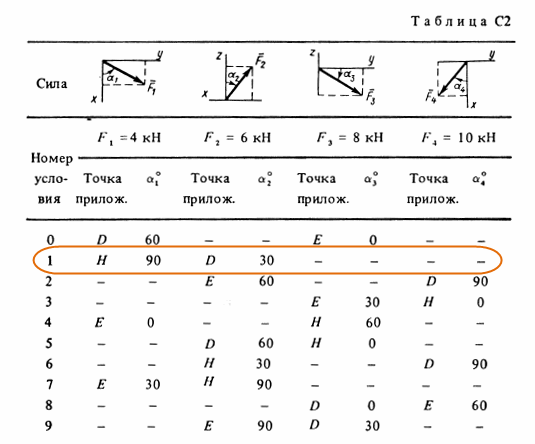
Однородная прямоугольная плита весом P = 5 кН со сторонами AB = 3l, BC = 2l закреплена в точке А сферическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем CC' (рис. С2.0 – С2.9). На плиту действуют пара сил с моментом M = 6 кН·м, лежащая в плоскости плиты, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С2; при этом силы F1 и F4 лежат в плоскостях, параллельных плоскости xy, сила F2 – в плоскости, параллельной xz, сила F3 – в плоскости, параллельной yz. Точки приложения сил (D, E, H) находятся в серединах сторон плиты. Определить реакции связей в точках A, B и C. При подсчетах принять l = 0,8 м.
 |
 |
Решение задачи по термеху K1-01 методичка Тарг 1988
Отправить также файл на почту |
Отправить также файл на почту |
Точка B движется в плоскости xy (рис. К1.0-К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: x = f1(t), y = f2(t), где x и y выражены в сантиметрах, t – в секундах. Найти уравнение траектории; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное ускорение и радиус кривизны в соответствующей точке траектории. Зависимость x = f1(t) указана непосредственно на рисунках, а зависимость y = f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4).
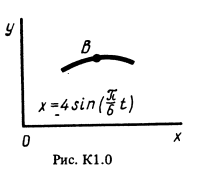 |
 |
Решение задачи по термеху K2-01 методичка Тарг 1988
Отправить также файл на почту |
Отправить также файл на почту |
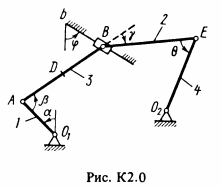
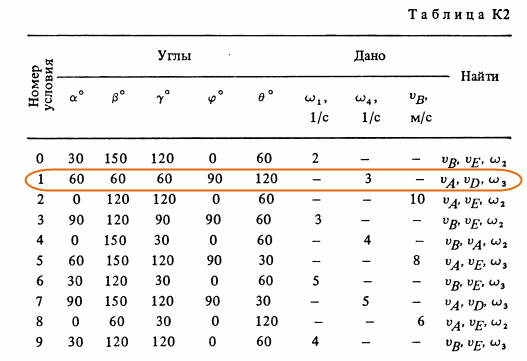
Плоский механизм состоит из стержней 1 – 4 и ползуна B, соединенных друг с другом и с неподвижными опорами O1 и O2 шарнирами (рис. К2.0-К2.9). Длины стержней: l1 = 0,4 м, l2 = 1,2 м, l3 = 1,4 м, l4 = 0,8 м. Положение механизма определяется углами α, β, γ, φ, θ, которые вместе с другими величинами заданы в табл. К2. Точка D на всех рисунках и точка К на рис. К2.7-К2.9 в середине соответствующего стержня. Определить величины, указанные в таблице в столбце «Найти». Найти также ускорение aA точки А стержня 1, если стержень 1 имеет в данный момент времени угловое ускорение ε1 = 10 с-2 Дуговые стрелки на рисунках показывают, как при построении чертежа должны откладываться соответствующие углы, т.е. по ходу или против хода часовой стрелки (например, угол γ на рис. 1 следует отложить от стержня DE против хода часовой стрелки, а на рис. 2 – от стержня AE по ходу часовой стрелки). Построение чертежа начинать со стержня, направление которого определяется углом α; ползун В и его направляющие для большей наглядности изобразить, как в примере К2 (см. рис. К2). Заданную угловую скорость считать направленной против хода часовой стрелки, а заданную скорость vB – от точки В к b.
 |
 |
Решение задачи по термеху K3-01 методичка Тарг 1988
Отправить также файл на почту |
Отправить также файл на почту |
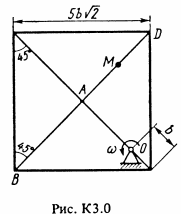
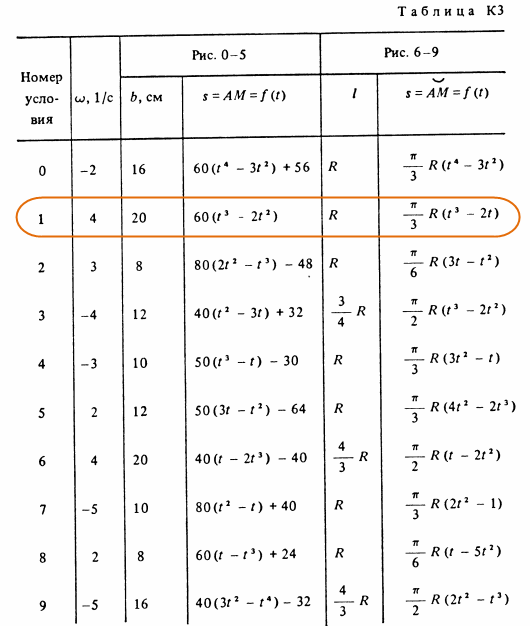
Прямоугольная пластина (рис. К3.0-К3.5) или круглая пластина радиусом R = 60 см (рис. К3.6-К3.9) вращается вокруг неподвижной оси с постоянной угловой скоростью ω, заданной в табл. К3 (при знаке минус направление ω противоположно показанному на рисунке). Ось вращения на рис. К3.0-К3.3 и К3.8, К3.9 перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. К3.4-К3.7 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве). По пластине вдоль прямой BD (рис. К3.0-К3.5) или по окружности радиуса R, т. е. по ободу пластины (рис. К3.6-К3.9), движется точка М. Закон ее относительного движения, выражаемый уравнением s = AM = f(t) (s – в сантиметрах, t – в секундах), задан в табл. К3 отдельно для рис. К3.0-К3.5 и для рис. К3.6-К3.9,при этом на рис. 6-9 s = AM и отсчитывается по дуге окружности; там же даны размеры b и l. На всех рисунках точка М показаны в положении, при котором s = AM > 0 (при s < 0 точка М находится по другую сторону от точки A). Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 с.
 |
 |
Решение задачи по термеху Д1-01 методичка Тарг 1988
Отправить также файл на почту |
Отправить также файл на почту |
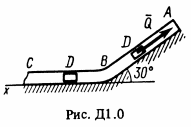
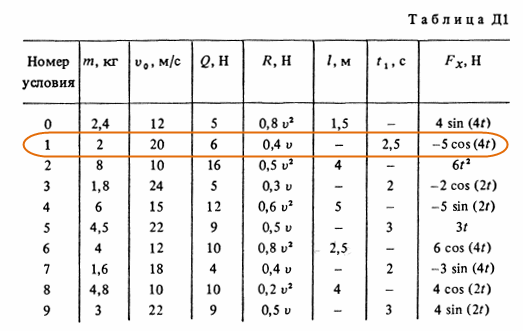
Груз D массой m, получив в точке А начальную скорость v0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0-Д1.9 табл. Д1). На рисунке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления среды R, зависит от скорости груза v (направлена против движения). В точке В груз, не изменяя значения своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует переменная сила F, проекция которой Fx на ось x задана в таблице. Считая груз материальной точкой и зная расстояние АВ = l или время t1 движения груза от точки А до точки В. Найти закон движения груза на участке ВС, т.е. x = f(t), где x = BD. Трением груза о трубу пренебречь.
 |
 |
Решение задачи по термеху Д2-01 методичка Тарг 1988
Отправить также файл на почту |
Отправить также файл на почту |
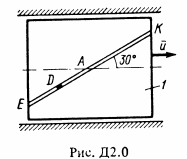
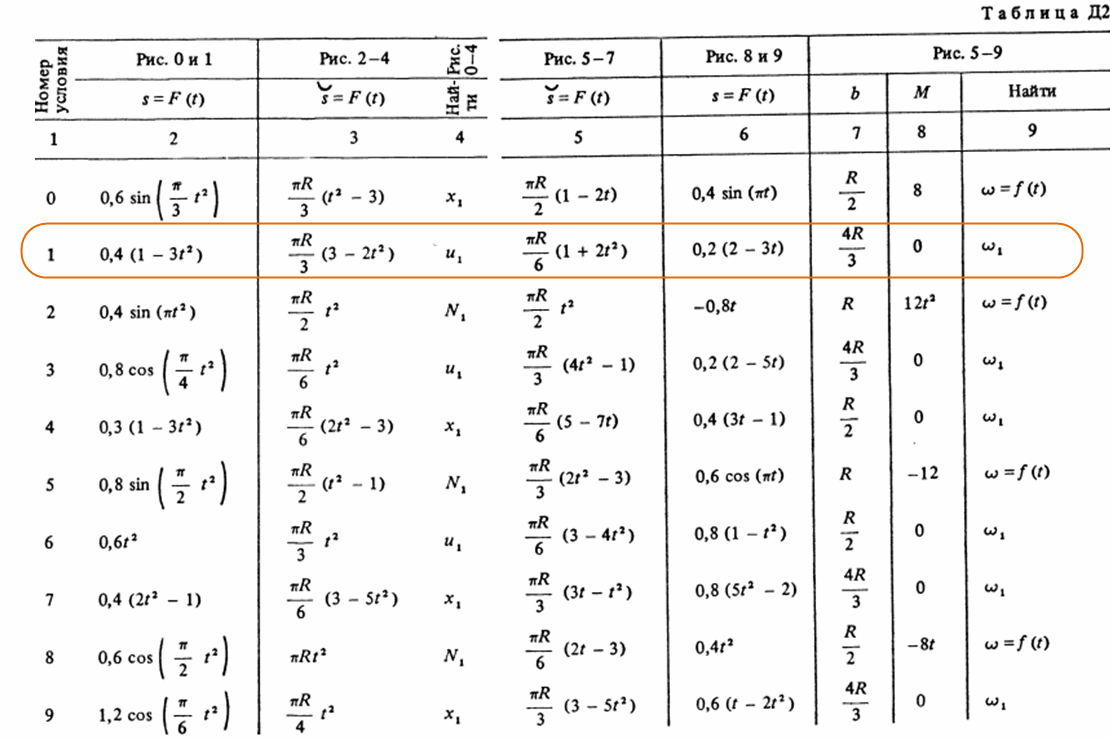
Механическая система состоит из прямоугольной вертикальной плиты 1 массой m1 = 24 кг и груза D массой m2 = 8 кг; плита или движется вокруг горизонтальных направляющий (рис. Д2.0-Д2.4), или вращается вокруг вертикальной оси z, лежащей в плоскости плиты (рис. Д2.5-Д2.9). В момент времени t0 = 0 груз начинает двигаться под действием внутренних сил по имеющемуся на плите желобу; закон его движения s = AD = F(t) задан в табл. Д2, где s выражено в метрах, t – в секундах. Форма желоба на рис. Д2.0, Д2.1, Д2.8, Д2.9 – прямолинейная (желоб КЕ), на рис. Д2.2-Д2.7 – окружность радиуса R = 0,8 м с центром в центре масс C1 плиты (s = AD на рис. Д2.2 - Д2.7 отсчитывается по дуге окружности). Плита (рис. Д2.0-Д2.4) имеет в момент t0 = 0 скорость v0 = 0. Плита (рис Д2.5-Д2.9) имеет в момент времени t0 = 0 угловую скорость ω0 = 8 с-1, и в этот момент на нее начинает действовать вращательный момент М (момент относительно оси), заданный в таблице в ньютонометрах и направленный как ω0 при М > 0 и в противоположную сторону при М < 0. Ось z проходит от центра C1 плиты на расстоянии b; размеры плиты показаны на рисунках. Считая грузы материальной точкой и пренебрегая всеми сопротивлениями, определить указанное в таблице в столбцах 4 и 9, где обозначено: в столбце 4 (относится к рис. Д2.0-Д2.4) x1 – перемещение плиты за время от t0 = 0 до t1 = 1 с, v – скорость плиты в момент времени t1 = 1 с, N – полная сила нормального давления плиты на направляющие в момент времени t = 1 с (указать, куда сила направлена); в столбце 9 (относится к рис. 5-9) ω1 – угловая скорость плиты в момент времени t1 = 1 с, ω = f(t) – угловая скорость плиты как функция времени. На всех рисунках груз показан в положении, при котором s = AD > 0; при x < 0 груз находится по другую сторону от точки А.
Решение задачи по термеху Д3-01 методичка Тарг 1988
Отправить также файл на почту |
Отправить также файл на почту |
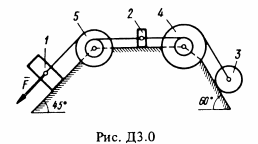
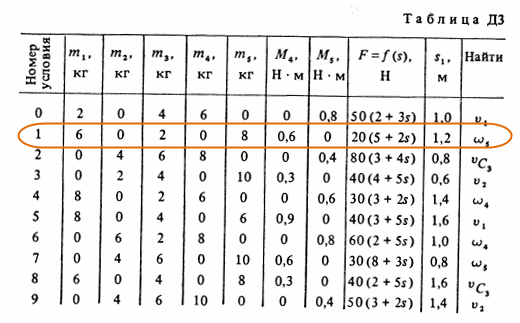
Механическая система состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость F = 0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R4 = 0,3 м, r4 = 0,1 м, R5 = 0,2 м, r5 = 0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу) (рис. Д3.0-Д3.9, табл. Д3). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Под действием силы F = f(x), зависящей от перемещения точки приложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивлений, равные соответственно M4 и M5. Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы F равно s1.
 |
 |
Решение задачи по термеху Д4-01 методичка Тарг 1988
Отправить также файл на почту |
Отправить также файл на почту |
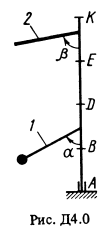
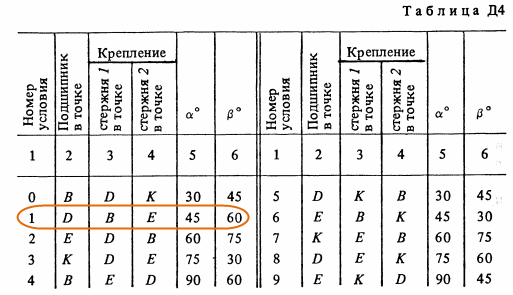
Вертикальный вал AK (рис. Д4.0-Д4.9, табл. Д4), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д4 в столбце 2 (AB = BD = DE = EK = b). К валу жестко прикреплены невесомый стержень 1 длиной l1 = 0,4 м с точечной массой m1 = 6 кг на конце и однородный стержень 2 длиной l2 = 0,6 м, имеющий массу m2 = 4 кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6. Пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять b = 0,4 м.
 |
 |
Решение задачи по термеху Д5-01 методичка Тарг 1988
Отправить также файл на почту |
Отправить также файл на почту |
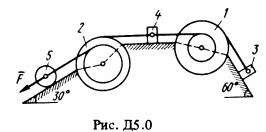
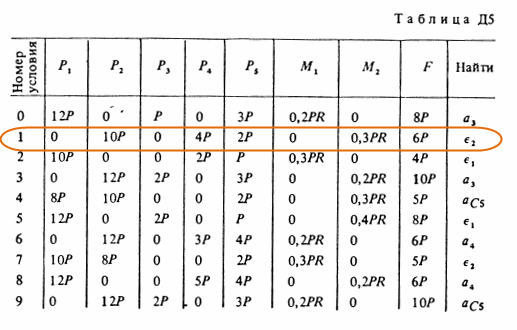
Механическая система состоит из ступенчатых шкивов 1 и 2 весом P1 и P2 с радиусами ступеней R1 = R, r1 = 0,4R; R2 = R, r3 = 0,8R (массу каждого шкива считать равномерно распределенной по его внешнему ободу); грузов 3, 4 и сплошного однородного цилиндрического катка 5 весом P3, P4, P5 соответственно (рис. Д5.0-Д5.9 табл. Д5). Тела системы соединены нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Грузы Скользят по плоскостям без трения, а катки катяться без скольжения. Кроме сил тяжести на одно из тел системы действует постоянная сила F, а на шкивы 1 и 2 при их вращении действуют постоянные моменты сил сопротивления, равные соответственно M1 и M2. Составить для данной системы уравнение Лагранжа и определить из него величину, указанную в таблице в столбце «Найти», где обозначено: ε1, ε2 – угловые ускорения шкивов 1 и 2; а3, а4, а С5 – ускорения грузов 3, 4 и центра масс катка 5 соответственно. Когда в задаче надо определить ε1, ε2, считать R = 0,25 м. Тот из грузов 3, 4 вес которого равен нулю, на чертеже не изображать. Шкивы 1 и 2 всегда входят в систему.
 |
 |