Задача по статистике S-2

Результаты исследований числа покупателей в универсаме в зависимости от времени работы приведены в таблице:

Можно ли утверждать при уровне значимости ? = 0,05, что число покупателей подчинено нормальному закону.

Решение:

Вычислим среднюю и дисперсию:

Определим выборочную среднюю:

Вычислим дисперсию:

Нулевую гипотезу сформулируем как утверждение, что случайная величина Х имеет нормальное распределение с указанными выше параметрами

Согласно критерию Пирсона, необходимо сравнить теоретические и эмпирические частоты. Определим теоретические частоты.

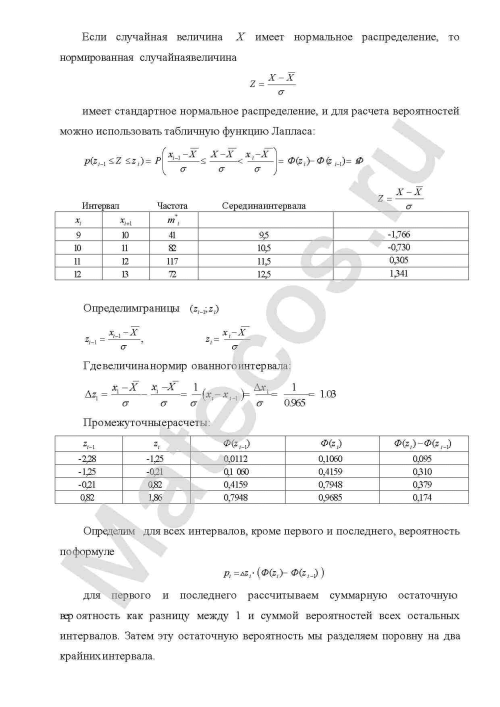
Если случайная величина Х имеет нормальное распределение, то нормированная случайная величина имеет стандартное нормальное распределение, и для расчета вероятностей можно использовать табличную функцию Лапласа:

Определим границы

Где величина нормированного интервала:

Промежуточные расчеты:

Определим для всех интервалов, кроме первого и последнего, вероятность по формуле

для первого и последнего рассчитываем суммарную остаточную вероятность как разницу между 1 и суммой вероятностей всех остальных интервалов. Затем эту остаточную вероятность мы разделяем поровну на два крайних интервала.

Далее определим теоретические частоты по формуле:

Расчеты внесем в таблицу:

Если нулевая гипотеза справедлива, то эмпирические частоты mi* должны быть близкими к теоретическим частотам mi.

Для оценки расхождения эмпирических и теоретических частот используем статистику

Результаты внесем в таблицу:

- распределение с числом степеней свободы v=q-1-k, где

q – число интервалов, на которые разбит весь диапазон изменения варьирующего признака (в нашем примере q=4),

k – число параметров генерального распределения, оцененных по данным выборки (в нашем примере k=2- по данным выборки оценены два параметра: средняя и среднее квадратическое отклонение ?)

Если ?²набл ? ?² , то гипотеза Но не отклоняется.

В нашем случае же ?²набл > ?² , то гипотеза Но отклоняется.